GradFinalLab RS

Go Back to All Lab Reports

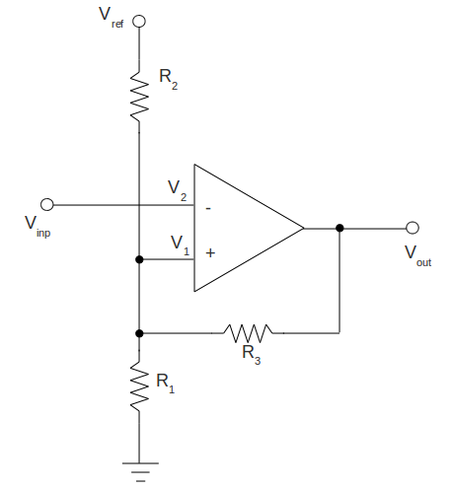
Construct a Schmitt Trigger using the 741 Op Amp

Draw the Schmitt Trigger circuit you constructed. Identify the values of all components

To construct the circuit above I am going to use the following components and voltages:

1. [math]R_1 = (1\pm)\ k\Omega[/math]
2. [math]R_2 = (1\pm)\ k\Omega[/math]
3. [math]R_3 = (10\pm)\ k\Omega[/math]
4. [math]\mbox{OP}\ \mbox{AMP}\ 741[/math]
5. [math]V_{ref} = (+15.00\pm0.01)\ V[/math]
6. [math]V_{cc} = (+15.00\pm0.01)\ V[/math]
7. [math]V_{ee} = (-15.01\pm0.01)\ V[/math]

Identify the input voltage threshold levels at which a [math] V_{in}[/math] will produce [math]V_{out} \approx V_{cc}[/math]

1) if the output is high:

[math]V_2 = \frac{R_{123}}{R_2}V_{ref} + \frac{R_{123}}{R_3}V_{cc}[/math]

2) if the output is low:

[math]V_2^' = \frac{R_{123}}{R_2}V_{ref} - \frac{R_{123}}{R_3}V_{cc}[/math]

where

[math]R_{123} = (R_1 || R_2 || R_3) = \frac{R_1 R_2 R_3}{R_1+R_2+R_3}[/math]

By substituting the actual values:

[math]R_{123} = (R_1 || R_2 || R_3) = \frac{R_1 R_2 R_3}{R_1+R_2+R_3}[/math]

[math]V_2 = \frac{R_{123}}{R_2}V_{ref} + \frac{R_{123}}{R_3}V_{cc}[/math]

[math]V_2^' = \frac{R_{123}}{R_2}V_{ref} - \frac{R_{123}}{R_3}V_{cc}[/math]

and doing math and handling the error propagation we end up with the following threshold voltages:

[math]V_2 = [/math]

[math]V_2^' =[/math]

Compare the threshold values to what is expected.

Go Back to All Lab Reports Forest_Electronic_Instrumentation_and_Measurement