Difference between revisions of "Lab 17 RS"
| (67 intermediate revisions by the same user not shown) | |||
| Line 15: | Line 15: | ||
{| border="2" cellpadding="8" cellspacing="0" | {| border="2" cellpadding="8" cellspacing="0" | ||
| − | |Characteristic | | + | |- |
| + | !scope="col" | Characteristic | ||
| + | !scope="col" | Symbol | ||
| + | !scope="col" | Min | ||
| + | !scope="col" | Max | ||
| + | !scope="col" | Unit | ||
|- | |- | ||
| Zero-Gate-Voltage Drain Current ||<math> I_{DSS}</math> || 2.0 || 20 || mAdc | | Zero-Gate-Voltage Drain Current ||<math> I_{DSS}</math> || 2.0 || 20 || mAdc | ||
|- | |- | ||
| − | | Gate-Source Cutoff Voltage|| <math>V_{GS(off)}</math> || - || -8.0 || Vdc | + | | Gate-Source Cutoff Voltage || <math>V_{GS(off)}</math> || - || -8.0 || Vdc |
|- | |- | ||
| − | | | + | | Total Device Dissipation @ <math>T_A=25^oC</math> |
| + | | <math>P_{max}</math> | ||
| + | | colspan="2" | 350 | ||
| + | | mW | ||
|- | |- | ||
| − | | | + | | Gait resistor |
| + | | <math>R_G</math> | ||
| + | | colspan="2" | 3.3 | ||
| + | | M<math>\Omega</math> | ||
|- | |- | ||
| − | | | + | | Drain resistor |
| + | | <math>R_D</math> | ||
| + | | colspan="2" | 1.0 | ||
| + | | k<math>\Omega</math> | ||
|- | |- | ||
| − | | ||<math>y_{fs}</math> || | + | | Forward Transfer Admittance || <math>y_{fs}</math> || 2000 || 7500 || <math>\mu</math>mhos |
|- | |- | ||
| − | | ||<math>y_{is}</math> || | + | | Input Admittance || <math>y_{is}</math> || - || 800 || <math>\mu</math>mhos |
| − | | | ||
| − | | ||<math> | ||
|- | |- | ||
| + | | Output Conductance || <math>y_{os}</math> || - || 200 || <math>\mu</math>mhos | ||
|} | |} | ||
| − | |||
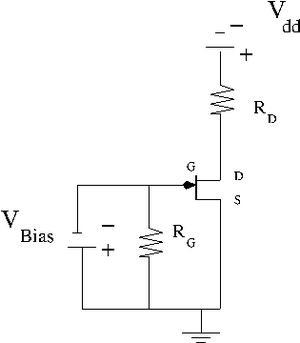
=2.) Construct the JFET circuit below.= | =2.) Construct the JFET circuit below.= | ||
| Line 48: | Line 60: | ||
<math>R_D = (0.968 \pm 0.002)\ k\Omega</math> | <math>R_D = (0.968 \pm 0.002)\ k\Omega</math> | ||
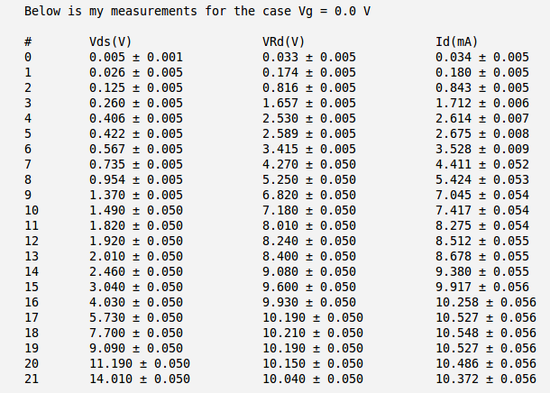
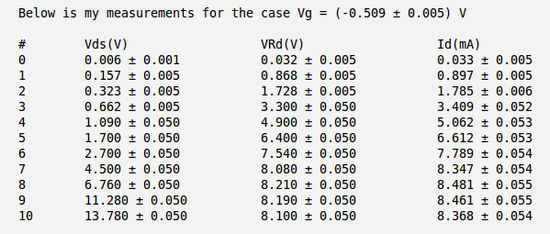
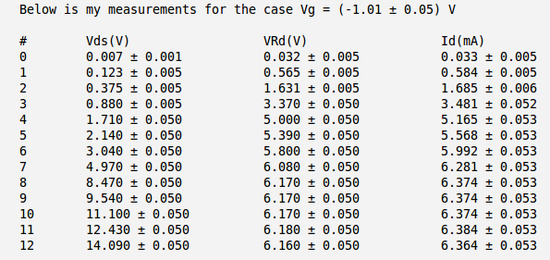
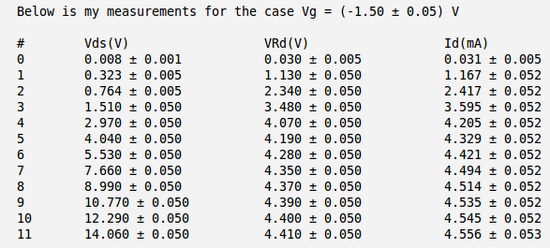
| − | Below is the table with my measurements of voltages <math>V_{DS}</math> and <math>V_{R_D}</math> and calculation of the current <math>I_D</math>. Here I have used the meter to measure directly the voltage drop between the drain and source <math>V_{DS}</math> and to measure the voltage drop on resistor <math>R_D</math>. | + | Below is the table with my measurements of voltages <math>V_{DS}</math> and <math>V_{R_D}</math> and calculation of the current <math>I_D</math>. Here I have used the meter to measure directly the voltage drop between the drain and source <math>V_{DS}</math> and to measure the voltage drop on resistor <math>R_D</math>. |
| + | So my calculated current becomes: | ||
| + | <math>I_D = \frac{V_{R_D}}{R_D}</math>. | ||
| + | |||
| + | |||
| + | [[File:Table01.png | 550 px]] | ||
| + | |||
| + | [[File:Table02.png | 550 px]] | ||
| + | |||
| + | [[File:Table03.png | 550 px]] | ||
| + | |||
| + | [[File:Table04.png | 550 px]] | ||
| + | |||
| + | |||
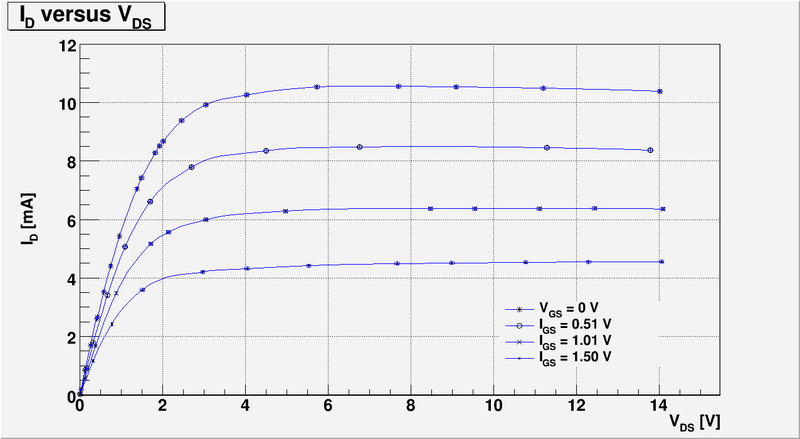
| + | And below I have plotted four curves <math>I_D</math> as function of <math>V_{DS}</math> for four different values of <math>V_{GS}</math> | ||
| + | |||
| + | |||
| + | [[File:L17 id vs vgs.png | 800 px]] | ||
=4.) Plot <math> I_D</math> -vs- <math>V_{GS}</math> (30 pnts)= | =4.) Plot <math> I_D</math> -vs- <math>V_{GS}</math> (30 pnts)= | ||
| + | |||
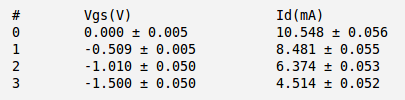
| + | For every measured <math>V_{GS}</math> values I have picked up the current <math>I_D</math> values in the middle of saturation region of each line as follow: | ||
| + | |||
| + | |||
| + | [[File:Table21.png | 500 px]] | ||
| + | |||
| + | |||
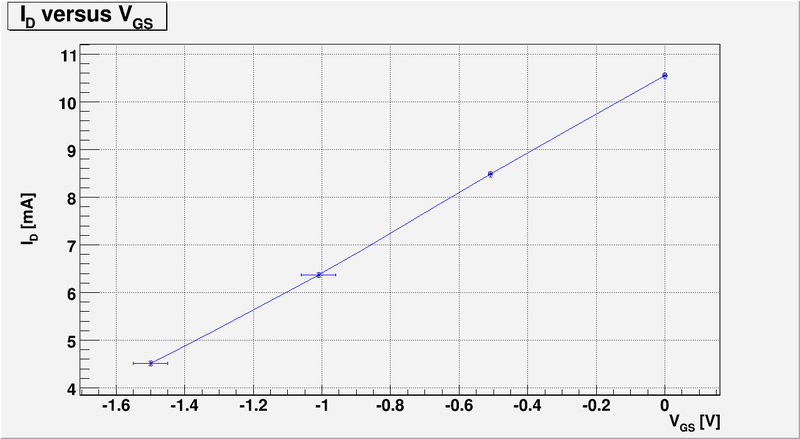
| + | And below is my plot of <math> I_D</math> -vs- <math>V_{GS}</math>: | ||
| + | |||
| + | |||
| + | [[File:L17 id vs vgs 21.png | 800 px]] | ||
| + | |||
| + | |||
=5.) Calculate <math>y_{fs}</math> for your JFET (20 pnts)= | =5.) Calculate <math>y_{fs}</math> for your JFET (20 pnts)= | ||
| + | |||
| + | For common source configuration JFET: | ||
| + | |||
| + | <math>y_{fs} \equiv \left ( \frac{\partial I_{out}}{\partial V_{in}} \right )_{V_{out}} = \left ( \frac{\partial I_D}{\partial V_{GS}} \right )_{V_{DS}}</math> | ||
| + | |||
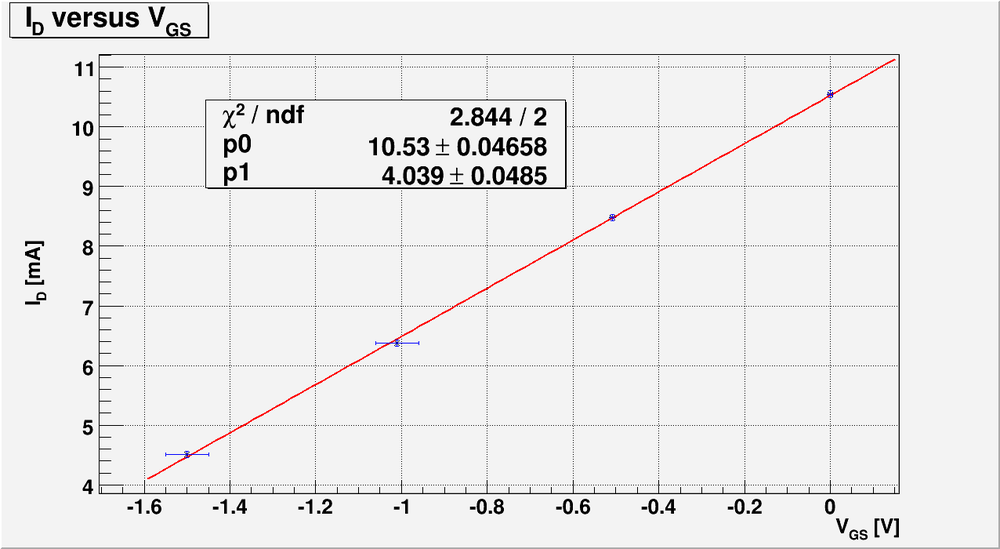
| + | So to calculate <math>y_{fs}</math> we need to know the functional dependence of <math>I_D(V_{GS})</math>. Lets approximate this function by line using my measurements and plot above: | ||
| + | |||
| + | [[File:L17 id vs vgs 22.png | 1000 px]] | ||
| + | |||
| + | The line equation is: | ||
| + | |||
| + | <math>I_D[mA] = (10.53 \pm 0.04)[mA] + (4.04 \pm 0.04)\cdot V_{GS}[V]</math> | ||
| + | |||
| + | Also note that this line equation was obtained using about the same voltage <math>V_{DS}</math> in saturation region from my first measurements of <math>I_D</math> as function of <math>V_{DS}</math> for four different values of <math>V_{GS}</math>. So we can take the partial derivative of <math>I_D</math> with respect to <math>V_{GS}</math> using the line equation above. Finally, | ||
| + | |||
| + | <math>y_{fs} \equiv \left ( \frac{\partial I_D}{\partial V_{GS}} \right )_{V_{DS}} = (4.04 \pm 0.04)\ \frac{mA}{V} = (4.04 \pm 0.04)\ mS</math> | ||
=Question= | =Question= | ||
| − | + | ==Does <math>y_{fs}</math> depend on <math>I_D</math>? (10 pnts)== | |
| + | |||
| + | No. As we can see from calculation above <math>y_{fs}</math> is constant and does not depend from <math>I_D</math>. That is true if we are working in saturation region where the functional dependence of <math>I_D</math> with respect to <math>V_{GS}</math> is line so | ||
| + | |||
| + | <math>y_{fs} \equiv \left ( \frac{\partial I_D}{\partial V_{GS}} \right )_{V_{DS}} = const</math> | ||
| + | |||
| + | If we are in active region of <math>I_D</math> as function of <math>V_{DS}</math> the functional form of <math>I_D</math> with respect to <math>V_{GS}</math> is not the line anymore and <math>y_{fs}</math> will depend on <math>I_D</math>. | ||
| + | |||
| + | |||
Latest revision as of 16:41, 13 April 2011
The JFET (Junction Field Effect Transistor n-channel)
File:JFET MPF102 DataSheet.pdf
1). Complete the table below for the JFET.
| Characteristic | Symbol | Min | Max | Unit |
|---|---|---|---|---|
| Zero-Gate-Voltage Drain Current | 2.0 | 20 | mAdc | |
| Gate-Source Cutoff Voltage | - | -8.0 | Vdc | |
| Total Device Dissipation @ | 350 | mW | ||
| Gait resistor | 3.3 | M | ||
| Drain resistor | 1.0 | k | ||
| Forward Transfer Admittance | 2000 | 7500 | mhos | |
| Input Admittance | - | 800 | mhos | |
| Output Conductance | - | 200 | mhos | |
2.) Construct the JFET circuit below.
3.) Plot measurements of -vs- by varying for = 0, 0.5, 1.0, 1.5 V. (40 pnts)
I have used the following resistors:
Below is the table with my measurements of voltages and and calculation of the current . Here I have used the meter to measure directly the voltage drop between the drain and source and to measure the voltage drop on resistor .
So my calculated current becomes:
.
And below I have plotted four curves as function of for four different values of
4.) Plot -vs- (30 pnts)
For every measured values I have picked up the current values in the middle of saturation region of each line as follow:
And below is my plot of -vs- :
5.) Calculate for your JFET (20 pnts)
For common source configuration JFET:
So to calculate we need to know the functional dependence of . Lets approximate this function by line using my measurements and plot above:
The line equation is:
Also note that this line equation was obtained using about the same voltage in saturation region from my first measurements of as function of for four different values of . So we can take the partial derivative of with respect to using the line equation above. Finally,
Question
Does depend on ? (10 pnts)
No. As we can see from calculation above is constant and does not depend from . That is true if we are working in saturation region where the functional dependence of with respect to is line so
If we are in active region of as function of the functional form of with respect to is not the line anymore and will depend on .
Go Back to All Lab Reports Forest_Electronic_Instrumentation_and_Measurement