Difference between revisions of "TF EIMLab6 Writeup"

From New IAC Wiki
Jump to navigation Jump to search
 
(21 intermediate revisions by the same user not shown)
Line 29: Line 29:
  
  
−
{| border="1"  |cellpadding="20" cellspacing="0
 
−
|-
 
−
| [[File:TF_EIM_L6_RC10t.png|200px]]||[[File:TF_EIM_L6RCt.png| 200px]] || [[File:TF_EIM_L6RC0.1t.png|200px]]
 
−
|-
 
−
|<math>R_1 C_1 =\tau/10 = 14.6 \mu s</math>|| <math>R_1 C_1 =\tau = 146 \mu s</math> || <math>R_1 C_1 =10 \tau = 1.460</math>ms
 
−
|}
 
  
  
Line 50: Line 44:
  
 
7.)Measure <math>V_{in} and V_{out}</math>.Sketch a picture comparing<math> V_{out}</math> and <math>V_{in}</math>.
 
7.)Measure <math>V_{in} and V_{out}</math>.Sketch a picture comparing<math> V_{out}</math> and <math>V_{in}</math>.
−
 
  
 
{| border="1"  |cellpadding="20" cellspacing="0  
 
{| border="1"  |cellpadding="20" cellspacing="0  
 
|-
 
|-
−
| [[File:TF_EIM_L6_RCLP10t.png|200px]]||[[File:TF_EIM_L6RCLPt.png| 200px]] || [[File:TF_EIM_L6RCLP0.1t.png|200px]]
+
| [[File:TF_EIM_L6_RC10t.png|200px]]||[[File:TF_EIM_L6RCt.png| 200px]] || [[File:TF_EIM_L6RC0.1t.png|200px]]
 +
|-
 +
|<math>RC =\tau/10 = 14.6 \mu s</math>|| <math>RC =\tau = 146 \mu s</math> || <math>RC =10 \tau = 1.460</math>ms
 
|-
 
|-
−
|<math>R_1 C_1 =\tau/10 = 14.6 \mu s</math>|| <math>R_1 C_1 =\tau = 146 \mu s</math> || <math>R_1 C_1 =10 \tau = 1.460</math>ms
+
|<math>RC >> \tau </math>|| <math>RC =\tau </math> || <math>RC << \tau </math>
 
|}
 
|}
  
Line 63: Line 58:
 
==Questions==
 
==Questions==
  
−
1.) What happens if than amplitude of <math>V_{in}</math> is doubled.
+
1.) What happens if the amplitude of <math>V_{in}</math> is doubled.
 +
 
 +
V_{out} is doubled if V_{in} is doubled.
  
 
2.) What happens if R is doubled and C is halved?
 
2.) What happens if R is doubled and C is halved?
 +
 +
Nothing, RC time constant remains the same.
  
 
=Integrator=
 
=Integrator=
Line 72: Line 71:
  
 
[[File:TF_EIM_PulsedRCLowpass.png | 400 px]]
 
[[File:TF_EIM_PulsedRCLowpass.png | 400 px]]
 +
 +
 +
{| border="1"  |cellpadding="20" cellspacing="0
 +
|-
 +
| [[File:TF_EIM_L6_RCLP10t.png|200px]]||[[File:TF_EIM_L6RCLPt.png| 200px]] || [[File:TF_EIM_L6RCLP0.1t.png|200px]]
 +
|-
 +
|<math>RC=\tau/10 = 14.6 \mu s</math>|| <math>RC =\tau = 146 \mu s</math> || <math>RC =10 \tau = 1.460</math>ms
 +
|-
 +
|<math>RC >> \tau </math>|| <math>RC =\tau </math> || <math>RC << \tau </math>
 +
|}
  
 
=Pulse Sharpener=
 
=Pulse Sharpener=
Line 90: Line 99:
 
:<math>R_{out}</math> = impedance of the function generator at output which produces V_{in}
 
:<math>R_{out}</math> = impedance of the function generator at output which produces V_{in}
 
: <math>C_{out}</math> = capacitor shorting the function generator output to ground (not shown in the above picture)
 
: <math>C_{out}</math> = capacitor shorting the function generator output to ground (not shown in the above picture)
 +
 +
: <math>e^{-t/\tau} = e^{-1} = =0.36788</math>
 +
 +
 +
<math>C_{out} = 1.210 \pm 0.005 \times 10^{-6} F</math>
 +
 +
I measure the times constant by looking how long it take the 2 Volt pulse to rise to (1-e^{-1}) =1.26 V
 +
 +
:<math>\tau = 60 \times 10^{-6}</math>
 +
 +
:<math>R = \tau/C = 60 \times 10^{-6} s/  1.210 \times 10^{-6} F =49.6 \Omega</math>
 +
 +
A second measurement:
 +
 +
:<math>\tau = 70 \times 10^{-6}</math>
 +
 +
:<math>R = \tau/C = 70 \times 10^{-6} s/  1.210 \times 10^{-6} F =57.9 \Omega</math>
 +
 +
I would say the input impedance of the BK precision function generator is about 50 <math>\Omega</math>.
  
 
2.) The output should be given by  
 
2.) The output should be given by  
Line 97: Line 125:
 
where
 
where
  
−
:<math>\tau^{\prime} = \left ( \frac{1}{R_1}+\frac{1}{R_2}\right ) C_1</math>
+
:<math>\tau^{\prime} = \left ( \frac{R_1 R}{R_1+ R}\right ) C_1</math>
  
 
3.) Make measurements of the rise time <math>\tau</math> and <math>\tau^{\prime}</math>.  The rise time is defined as the time it take the pulse to go from 10% of its max value to 90% of its max value.( 5 pnts.)
 
3.) Make measurements of the rise time <math>\tau</math> and <math>\tau^{\prime}</math>.  The rise time is defined as the time it take the pulse to go from 10% of its max value to 90% of its max value.( 5 pnts.)
  
−
4.) Compare the measurement of <math>\tau^{\prime}</math> to what you expected based on your measured values of <math>C_1</math>, <math>R_1</math> and<math> R_2</math>.( 15 pnts.)
+
4.) Compare the measurement of <math>\tau^{\prime}</math> to what you expected based on your measured values of <math>C_1</math>, <math>R_1</math> and<math> R</math>.( 15 pnts.)
  
 
==Questions==
 
==Questions==
  
−
1.) Qualitatify, why is <math>\tau^{\prime} < \tau</math>?( 10 pnts.)
+
1.) Qualitativly, why is <math>\tau^{\prime} < \tau</math>?( 10 pnts.)
 +
 
 +
:<math>\tau^{\prime} = \left ( \frac{R_1 R}{R_1+ R}\right ) C_1 =  \left ( \frac{R_1 }{R_1+ R}\right )\tau</math>
 +
 
 +
The circuit is a filter that passes high frequency changes in V but attenating low frequency.  Or in other words the power gets pushed intot he high frequncy band. 
  
 
2.) How is <math>V_{out}</math> worse than <math>V_{in}</math>( 10 pnts.)
 
2.) How is <math>V_{out}</math> worse than <math>V_{in}</math>( 10 pnts.)
 +
 +
:<math>V_{out} = V_0^{\prime} \left ( 1 - e^{-t/\tau^{\prime}}\right ) =  \left ( \frac{R_1 }{R_1+ R}\right ) V_0\left ( 1 - e^{-t/\tau^{\prime}}\right )</math>
  
  
 
[[Forest_Electronic_Instrumentation_and_Measurement]]
 
[[Forest_Electronic_Instrumentation_and_Measurement]]

Latest revision as of 17:38, 27 March 2011

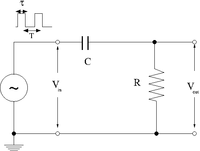
Lab 6 Pulses and RC Filters

Differentiator

1.) Adjust the pulse generator to output square pulses which at [math]\tau[/math] sec in time.

Possible capacitors

[math]C_1 = 1 \times 10^{-6} F[/math]
[math]C_2 = 10.24 \times 10^{-9} F[/math]

Possible Resistors

[math]R_1 = 1 \times 10^3 \Omega[/math]
[math]R_2 = 14.35 \times 10^{3} \Omega[/math]


[math]R_1 C_1 = \tau_1 = (1 \times 10^3 \Omega ) (1 \times 10^{-6} F )= 0.001[/math] s
[math]R_1 C_1 = \tau_2 = (14.35 \times 10^{3} \Omega)(10.24 \times 10^{-9} F )= 1.46 \times 10^{-4}[/math]
[math]\omega_1 = 100 rad/sec \Rightarrow \nu_1 = 100/2\pi = 16 Hz[/math]
[math]\omega_2 = 6805 rad/sec \Rightarrow \nu_2 = 1083 Hz[/math]

tek012

[math]R_1 C_1 =10 \tau_2 = 1460 \mu s[/math]



2.)Construct the circuit below selecting an RC combination such that RC [math]\approx[/math] 1/10

TF EIM Lab6b.png

3.)Measure[math] V_{in}[/math] and [math]V_{out}[/math]. Sketch a picture comparing[math] V_{out}[/math] and [math]V_{in}[/math].

4.) Change the pulse width such that [math]RC = \tau[/math]

5.)Measure[math] V_{in}[/math] and [math]V_{out}[/math].Sketch a picture comparing[math] V_{out}[/math] and [math]V_{in}[/math].

6.) Change the pulse width such that[math] RC = 10 \tau[/math]

7.)Measure [math]V_{in} and V_{out}[/math].Sketch a picture comparing[math] V_{out}[/math] and [math]V_{in}[/math].

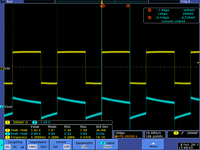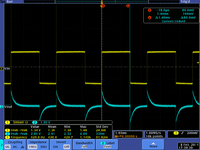
TF EIM L6 RC10t.png TF EIM L6RCt.png TF EIM L6RC0.1t.png
[math]RC =\tau/10 = 14.6 \mu s[/math] [math]RC =\tau = 146 \mu s[/math] [math]RC =10 \tau = 1.460[/math]ms
[math]RC \gt \gt \tau [/math] [math]RC =\tau [/math] [math]RC \lt \lt \tau [/math]


Questions

1.) What happens if the amplitude of [math]V_{in}[/math] is doubled.

V_{out} is doubled if V_{in} is doubled.

2.) What happens if R is doubled and C is halved?

Nothing, RC time constant remains the same.

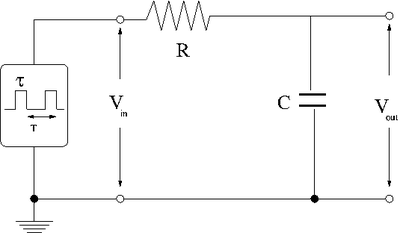
Integrator

Now repeat the above experiment with the resistor and capacitor swapped to form the low pass circuit below.

TF EIM PulsedRCLowpass.png


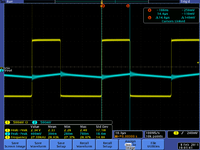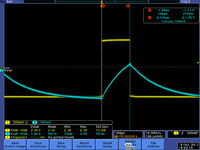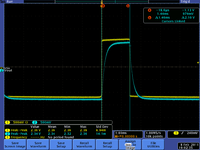
TF EIM L6 RCLP10t.png TF EIM L6RCLPt.png TF EIM L6RCLP0.1t.png
[math]RC=\tau/10 = 14.6 \mu s[/math] [math]RC =\tau = 146 \mu s[/math] [math]RC =10 \tau = 1.460[/math]ms
[math]RC \gt \gt \tau [/math] [math]RC =\tau [/math] [math]RC \lt \lt \tau [/math]

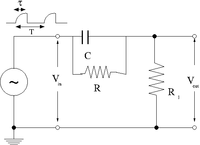
Pulse Sharpener

The goal of this section is to demonstrate how well the circuit below can sharpen an input pulse

TF EIM Lab6a.png

1.) The first step is to create an input pulse which is rounded, similar to the output of the integrator circuit when RC = 10 [math]\tau[/math]. You can do this using a capacitor shorted across the output of the pulse generator. This will essential be coupled to the input impedance of the pulse generator and form a low pass circuit.

As a result the input voltage is given as

[math]V_{in} = V_0 \left ( 1 - e^{-t/\tau}\right )[/math]

where

[math]\tau=R_{out} C_{out}[/math]
[math]R_{out}[/math] = impedance of the function generator at output which produces V_{in}
[math]C_{out}[/math] = capacitor shorting the function generator output to ground (not shown in the above picture)
[math]e^{-t/\tau} = e^{-1} = =0.36788[/math]


[math]C_{out} = 1.210 \pm 0.005 \times 10^{-6} F[/math]

I measure the times constant by looking how long it take the 2 Volt pulse to rise to (1-e^{-1}) =1.26 V

[math]\tau = 60 \times 10^{-6}[/math]
[math]R = \tau/C = 60 \times 10^{-6} s/ 1.210 \times 10^{-6} F =49.6 \Omega[/math]

A second measurement:

[math]\tau = 70 \times 10^{-6}[/math]
[math]R = \tau/C = 70 \times 10^{-6} s/ 1.210 \times 10^{-6} F =57.9 \Omega[/math]

I would say the input impedance of the BK precision function generator is about 50 [math]\Omega[/math].

2.) The output should be given by

[math]V_{out} = V_0^{\prime} \left ( 1 - e^{-t/\tau^{\prime}}\right )[/math]

where

[math]\tau^{\prime} = \left ( \frac{R_1 R}{R_1+ R}\right ) C_1[/math]

3.) Make measurements of the rise time [math]\tau[/math] and [math]\tau^{\prime}[/math]. The rise time is defined as the time it take the pulse to go from 10% of its max value to 90% of its max value.( 5 pnts.)

4.) Compare the measurement of [math]\tau^{\prime}[/math] to what you expected based on your measured values of [math]C_1[/math], [math]R_1[/math] and[math] R[/math].( 15 pnts.)

Questions

1.) Qualitativly, why is [math]\tau^{\prime} \lt \tau[/math]?( 10 pnts.)

[math]\tau^{\prime} = \left ( \frac{R_1 R}{R_1+ R}\right ) C_1 = \left ( \frac{R_1 }{R_1+ R}\right )\tau[/math]

The circuit is a filter that passes high frequency changes in V but attenating low frequency. Or in other words the power gets pushed intot he high frequncy band.

2.) How is [math]V_{out}[/math] worse than [math]V_{in}[/math]( 10 pnts.)

[math]V_{out} = V_0^{\prime} \left ( 1 - e^{-t/\tau^{\prime}}\right ) = \left ( \frac{R_1 }{R_1+ R}\right ) V_0\left ( 1 - e^{-t/\tau^{\prime}}\right )[/math]


Forest_Electronic_Instrumentation_and_Measurement

Retrieved from "https://wiki.iac.isu.edu/index.php?title=TF_EIMLab6_Writeup&oldid=59617"