Difference between revisions of "Lab 10 RS"
| (39 intermediate revisions by the same user not shown) | |||
| Line 18: | Line 18: | ||
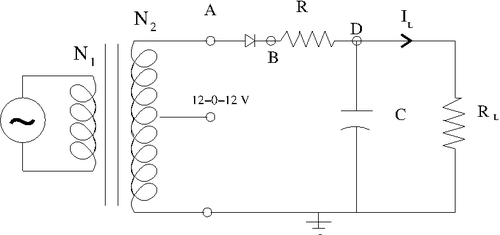
1.)Consider building circuit below. | 1.)Consider building circuit below. | ||
| − | [[File:TF_EIM_Lab10_HW_Rectifier.png| | + | [[File:TF_EIM_Lab10_HW_Rectifier.png| 500 px]] |
| − | Determine the components needed in order to make the output ripple have a <math>\Delta V</math> less than 1 Volt. | + | '''Determine the components needed in order to make the output ripple have a <math>\Delta V</math> less than 1 Volt.''' |
The output ripple can be found by <math>\Delta V=\frac{I\Delta t}{C}</math> | The output ripple can be found by <math>\Delta V=\frac{I\Delta t}{C}</math> | ||
| − | Taking | + | Taking AC signal from outlet equals to <math>60\ Hz</math> my input pulse width is <math>\Delta t = \frac{1}{60\ sec} = 17\ ms</math> and using say <math>C = 2.2\ uF</math> I need my current to be: |
| − | <math>I \le \frac{1\ V \cdot 2.2\ uF}{17\ | + | <math>I \le \frac{1\ V \cdot 2.2\ uF}{17\ ms} \le 0.129\ mA</math> |
| + | Taking <math>R \ge 100\ k\Omega \Rightarrow I = \frac{12\ V}{100\ k\Omega} \le 0.12\ mA</math> | ||
| − | + | that satisfy the condition above for current so my output ripple becomes less than 1 Volts. | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''List the components below and show your instructor the output observed on the scope and sketch it below.''' | ||
| − | I have used the following components | + | I have used the following components: |
<math>R = 96.9\ k\Omega</math> | <math>R = 96.9\ k\Omega</math> | ||
| Line 37: | Line 43: | ||
<math>R_{scope} = 1\ M\Omega</math> | <math>R_{scope} = 1\ M\Omega</math> | ||
<math>C = 2.2\ uF</math> | <math>C = 2.2\ uF</math> | ||
| − | + | <math>\mbox{Zener}\ \mbox{Diode}\ 4.7\ V</math> | |
| − | |||
| − | |||
| − | |||
| − | <math>\ | ||
| − | |||
| Line 56: | Line 57: | ||
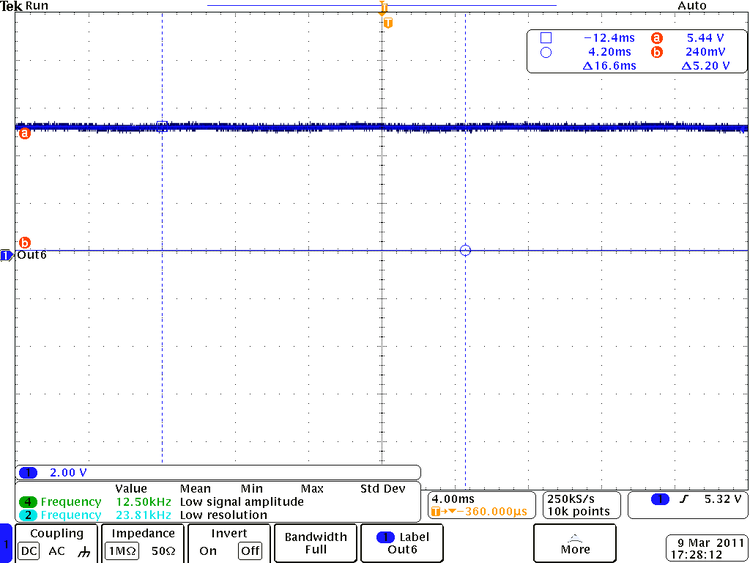
| + | [[File:Tek00047.png | 800 px]] | ||
| − | |||
| + | As we can see from the sketch above my output voltage has ripple about <math>\Delta V = 0.710\ V</math>, ripple time period is the same as input time <math>\Delta t = 16.6\ ms</math>, and the output DC voltage is about <math>V_{out} = 0.6\ V</math> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <br><br><br><br><br><br><br><br><br><br> | ||
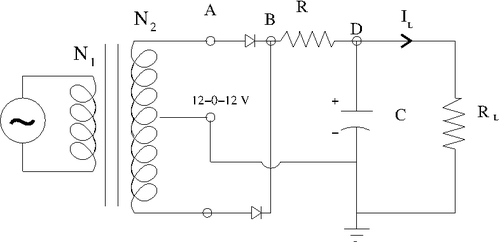
=Full-Wave Rectifier Circuit= | =Full-Wave Rectifier Circuit= | ||
| − | [[File:TF_EIM_Lab10_FW_Rectifier.png| | + | [[File:TF_EIM_Lab10_FW_Rectifier.png| 500 px]] |
| + | |||
| + | |||
| + | '''Determine the components needed in order to make the above circuit's output ripple have a <math>\Delta V</math> less than 0.5 Volt.''' | ||
| + | |||
| + | |||
| + | The output ripple in this case can be found by <math>\Delta V=\frac{I (\Delta t/2)}{C}</math> | ||
| + | |||
| + | Because we are now using <math>(\Delta t/2)</math> instead of <math>(\Delta t)</math> than in previous case for half-wave rectifier theoretiacally we will be able to make <math>\Delta V</math> two times less then in previous case just by using exactly the same elements and input parameters as before. But here I realized by experiment that my Zener diode has low power limit and for this kind of circuit I need to use more powerful diode. Instead of 4.7 Zener Diode which has power limit 0.5 W I used rectifier diode 1N4001 which has power limit 50 W. | ||
| + | |||
| + | |||
| + | '''List the components below and show your instructor the output observed on the scope and sketch it below.''' | ||
| + | |||
| + | I have used the following components: | ||
| + | |||
| + | <math>R = 96.9\ k\Omega</math> | ||
| + | <math>R_L = 98.7\ k\Omega</math> | ||
| + | <math>R_{scope} = 1\ M\Omega</math> | ||
| + | <math>C = 2.2\ uF</math> | ||
| + | <math>2\ \mbox{1N4001}\ \mbox{Diode}\ 50\ W</math> | ||
| + | |||
| + | |||
| + | Because now I need to replace <math>\Delta t</math> by <math>(\Delta t)/2</math> my output voltage now becomes two times less: | ||
| + | |||
| + | <math>\Delta V = \frac{0.9\ V}{2} = 0.45\ V</math> | ||
| + | |||
| + | Now my DC output voltage becomes about <math>V = 5.2\ V</math> and ripple you can not even see for that scale. | ||
| + | |||
| + | [[File:Tek00053.png | 750 px]] | ||
| + | |||
| + | |||
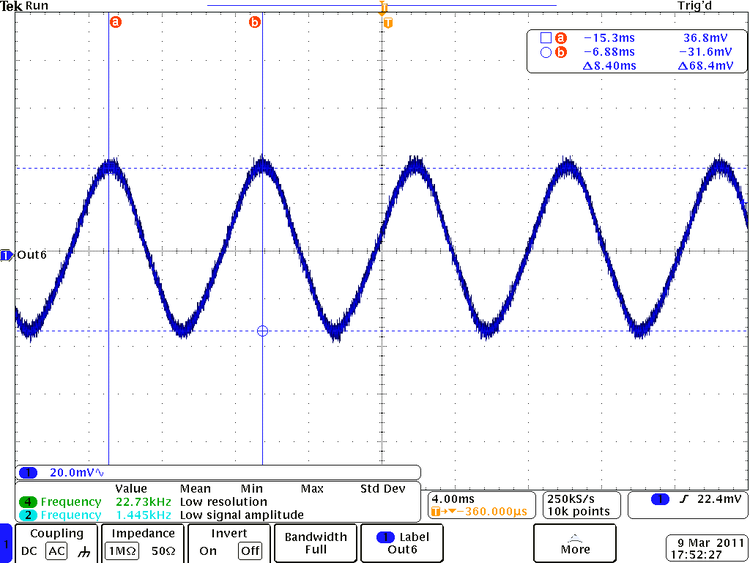
| + | To see ripple I used the AC mode of scope and they are plotted below. As we can see from this sketch my output voltage has ripple about <math>\Delta V = 68.4\ mV</math>, and the ripple time period now is two times less than input time period and is about <math>\Delta t = 8.4\ ms</math>. | ||
| + | |||
| + | [[File:Tek00054.png | 750 px]] | ||
| + | |||
| − | + | Now I have almost perfect output DC current with small ripple. | |
| − | |||
[https://wiki.iac.isu.edu/index.php/Electronics_RS Go Back to All Lab Reports] [[Forest_Electronic_Instrumentation_and_Measurement]] | [https://wiki.iac.isu.edu/index.php/Electronics_RS Go Back to All Lab Reports] [[Forest_Electronic_Instrumentation_and_Measurement]] | ||
Latest revision as of 20:03, 11 March 2011
Lab 10 Unregulated power supply
Use a transformer for the experiment.
here is a description of the transformer.
File:TF EIM 241 transformer.pdf
Half-Wave Rectifier Circuit
1.)Consider building circuit below.
Determine the components needed in order to make the output ripple have a less than 1 Volt.
The output ripple can be found by
Taking AC signal from outlet equals to my input pulse width is and using say I need my current to be:
Taking
that satisfy the condition above for current so my output ripple becomes less than 1 Volts.
List the components below and show your instructor the output observed on the scope and sketch it below.
I have used the following components:
The current through the circuit can be found as
where
.
And the current becomes
So my output ripple becomes
As we can see from the sketch above my output voltage has ripple about , ripple time period is the same as input time , and the output DC voltage is about
Full-Wave Rectifier Circuit
Determine the components needed in order to make the above circuit's output ripple have a less than 0.5 Volt.
The output ripple in this case can be found by
Because we are now using instead of than in previous case for half-wave rectifier theoretiacally we will be able to make two times less then in previous case just by using exactly the same elements and input parameters as before. But here I realized by experiment that my Zener diode has low power limit and for this kind of circuit I need to use more powerful diode. Instead of 4.7 Zener Diode which has power limit 0.5 W I used rectifier diode 1N4001 which has power limit 50 W.
List the components below and show your instructor the output observed on the scope and sketch it below.
I have used the following components:
Because now I need to replace by my output voltage now becomes two times less:
Now my DC output voltage becomes about and ripple you can not even see for that scale.
To see ripple I used the AC mode of scope and they are plotted below. As we can see from this sketch my output voltage has ripple about , and the ripple time period now is two times less than input time period and is about .
Now I have almost perfect output DC current with small ripple.
Go Back to All Lab Reports Forest_Electronic_Instrumentation_and_Measurement