Lab 10 RS

Go Back to All Lab Reports

Lab 10 Unregulated power supply

Use a transformer for the experiment.

here is a description of the transformer.

File:TF EIM 241 transformer.pdf

File:IN5230-B-T DataSheet.pdf

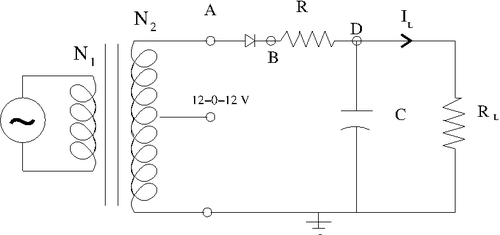
Half-Wave Rectifier Circuit

1.)Consider building circuit below.

Determine the components needed in order to make the output ripple have a $\Delta V$ less than 1 Volt.

The output ripple can be found by $\Delta V=\frac{I\Delta t}{C}$

Taking AC signal from outlet equals to $60\ Hz$ my input pulse width is $\Delta t = \frac{1}{60\ sec} = 17\ ms$ and using say $C = 2.2\ uF$ I need my current to be:

$I \le \frac{1\ V \cdot 2.2\ uF}{17\ ms} \le 0.129\ mA$

Taking $R \ge 100\ k\Omega \Rightarrow I = \frac{12\ V}{100\ k\Omega} \le 0.12\ mA$

that satisfy the condition above for current so my output ripple becomes less than 1 Volts.

List the components below and show your instructor the output observed on the scope and sketch it below.

I have used the following components:

[math]R = 96.9\ k\Omega[/math]
[math]R_L = 98.7\ k\Omega[/math]
[math]R_{scope} = 1\ M\Omega[/math]
[math]C = 2.2\ uF[/math]

and the following input parameters:

[math]\Delta t = 17\ ms[/math]
[math]V_{in} = 12\ V[/math]

The current through the circuit can be found as $I = \frac{V_{in}}{R_{tot}}$

where $R_{tot} = R + \left|\frac{R_L \cdot \frac{1}{j\omega C}}{R_L + \frac{1}{j\omega C}} \right| = R + \sqrt{ \left(\frac{R_L}{1 + j\omega CR_L}\right)\left(\frac{R_L}{1 + j\omega CR_L}\right)^* } = R + \sqrt{ \left(\frac{R_L^2}{1 + (\omega CR_L)^2}\right) }$

$= 96.9\ k\Omega + \sqrt{\frac{(98.7\ k\Omega)^2 }{1 + (2\pi\ 60\ sec^{-1})^2(2.2\ uF)^2 (98.7\ k\Omega)^2} }= 96.9\ k\Omega + 1.2\ k\Omega =98.1\ k\Omega$.

And the current becomes $I = \frac{12\ V}{98.1\ k\Omega} = 0.122\ mA$

So my output ripple becomes $\Delta V = \frac{0.122\ mA \cdot 17\ ms}{2.2\ uF} = 0.9 V$

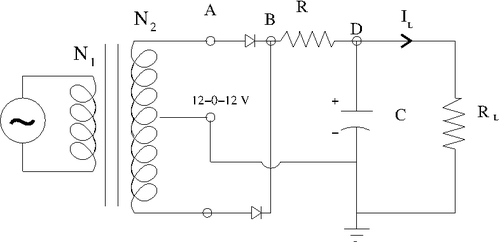
Full-Wave Rectifier Circuit

Determine the components needed in order to make the above circuit's output ripple have a $\Delta V$ less than 0.5 Volt.

The output ripple in this case can be found by $\Delta V=\frac{I (\Delta t/2)}{C}$

Because we are now using $(\Delta t/2)$ instead of $(\Delta t)$ than in previous case for half-wave rectifier theoretiacally we will be able to make $\Delta V$ two times less then in previous case just by using exactly the same ellements and input parameters as before:

List the components below and show your instructor the output observed on the scope and sketch it below.

Go Back to All Lab Reports Forest_Electronic_Instrumentation_and_Measurement