Lab 10 RS

Go Back to All Lab Reports

Lab 10 Unregulated power supply

Use a transformer for the experiment.

here is a description of the transformer.

File:TF EIM 241 transformer.pdf

File:IN5230-B-T DataSheet.pdf

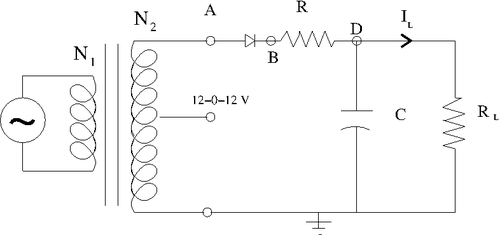
Half-Wave Rectifier Circuit

1.)Consider building circuit below.

Determine the components needed in order to make the output ripple have a [math]\Delta V[/math] less than 1 Volt.

The output ripple can be found by [math]\Delta V=\frac{I\Delta t}{C}[/math]

Taking AC signal from outlet equals to [math]60\ Hz[/math] my input pulse width is [math]\Delta t = \frac{1}{60\ sec} = 17\ ms[/math] and using say [math]C = 2.2\ uF[/math] I need my current to be:

[math]I \le \frac{1\ V \cdot 2.2\ uF}{17\ ms} \le 0.129\ mA[/math]

Taking [math]R \ge 100\ k\Omega \Rightarrow I = \frac{12\ V}{100\ k\Omega} \le 0.12\ mA[/math]

that satisfy the condition above so my output ripple becomes less than 1 Volts.

List the components below and show your instructor the output observed on the scope and sketch it below.

I have used the following components:

[math]R = 96.9\ k\Omega[/math]
[math]R_L = 98.7\ k\Omega[/math]
[math]R_{scope} = 1\ M\Omega[/math]
[math]C = 2.2\ uF[/math]

and the following input parameters:

[math]\Delta t = 17\ ms\ which\ corresponds\ to\ 60\ Hz[/math]
[math]V_{in} = 12\ V[/math]

The current through the circuit can be found as [math]I = \frac{V_{in}}{R_{tot}}[/math]

where [math] R_{tot} = R + \left|\frac{R_L \cdot \frac{1}{j\omega C}}{R_L + \frac{1}{j\omega C}} \right| = R + \sqrt{ \left(\frac{R_L}{1 + j\omega CR_L}\right)\left(\frac{R_L}{1 + j\omega CR_L}\right)^* } = R + \sqrt{ \left(\frac{R_L^2}{1 + (\omega CR_L)^2}\right) } [/math]

[math] = 96.9\ k\Omega + \sqrt{\frac{(98.7\ k\Omega)^2 }{1 + (2\pi\ 60\ sec^{-1})^2(2.2\ uF)^2 (98.7\ k\Omega)^2} }= 96.9\ k\Omega + 1.2\ k\Omega =98.1\ k\Omega[/math].

And the current becomes [math]I = \frac{12\ V}{98.1\ k\Omega} = 0.122\ mA[/math]

So my output ripple becomes [math]\Delta V = \frac{0.122\ mA \cdot 17\ ms}{2.2\ uF} = 0.9 V[/math]

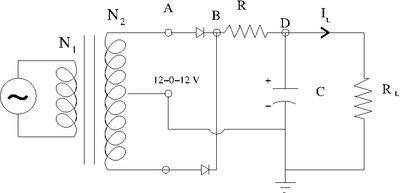
Full-Wave Rectifier Circuit

Determine the components needed in order to make the above circuit's output ripple have a [math]\Delta V[/math] less than 0.5 Volt.

List the components below and show your instructor the output observed on the scope and sketch it below.

Go Back to All Lab Reports Forest_Electronic_Instrumentation_and_Measurement