Difference between revisions of "Lab 5 RS"
Jump to navigation
Jump to search
| Line 16: | Line 16: | ||
:<math>C=1.024\ \mu F</math> | :<math>C=1.024\ \mu F</math> | ||
:<math>R=0.989\ k \Omega</math> | :<math>R=0.989\ k \Omega</math> | ||
| + | :<math>R_L=2.5 \Omega</math> | ||
| + | So the resonance frequency is <math>\omega_0=\frac{1}{\sqrt{33\ \mu H \cdot 1.024\ \mu F</math>}} = 172 \cdot 10^3\ \frac{\mbox{rad}}{\mbox{sec}}</math> | ||
| − | + | :<math>f=\frac{\omega_0}{2\pi} = 27.4\ \mbox{kHz}</math> | |
| − | + | And | |
| − | + | :<math>/mbox{Q} = \frac{1}{\mbox{R}} \sqrt{\fraq{\mbox{L}}{\mbox{C}}} = 2.27</math> | |
| − | |||
| − | |||
| − | |||
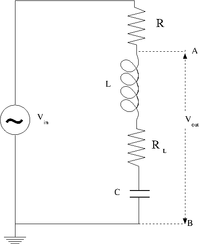
==Construct the LC circuit using a non-polar capacitor== | ==Construct the LC circuit using a non-polar capacitor== | ||
Revision as of 20:58, 3 February 2011
- LC Resonance circuits
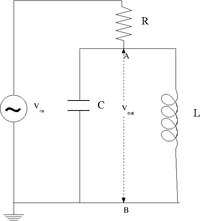
The LC circuit
Design a parallel LC resonant circuit with a resonant frequency between 50-200 kHz. use = 10 - 100 , R = 1k
I choose the following values for and :
So the resonance frequency is }} = 172 \cdot 10^3\ \frac{\mbox{rad}}{\mbox{sec}}</math>
And
Construct the LC circuit using a non-polar capacitor
Measure the Gain as a function of frequency. (25 pnts)
Compare the measured and theoretical values of the resonance frequency () (10 pnts)
Questions
1.Is there a value of in which at resonance. What is the value?(5 pnts)