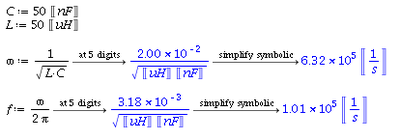Difference between revisions of "Lab 5 RS"
Jump to navigation
Jump to search
| Line 11: | Line 11: | ||
:<math>\omega_0=\frac{1}{\sqrt{\mbox{LC}}}</math> | :<math>\omega_0=\frac{1}{\sqrt{\mbox{LC}}}</math> | ||
| − | I choose the following values for <math>\mbox{ | + | I choose the following values for <math>\mbox{L}</math> and <math>\mbox{C}</math>: |
| + | |||
| + | :<math>L=33\ \mu H</math> | ||
| + | :<math>C=1.024\ \mu F</math> | ||
| + | :<math>R=0.989\ k \Omega</math> | ||
| − | |||
| − | |||
So the resonance frequency is <math>\omega_0=\frac{1}{\sqrt{aaa\ \Omega\ bbb\ \mu F }} = ccc\ \frac{\mbox{rad}}{\mbox{sec}}</math> | So the resonance frequency is <math>\omega_0=\frac{1}{\sqrt{aaa\ \Omega\ bbb\ \mu F }} = ccc\ \frac{\mbox{rad}}{\mbox{sec}}</math> | ||
| Line 24: | Line 26: | ||
[[File:L4 LC.png | 400 px]] | [[File:L4 LC.png | 400 px]] | ||
| − | |||
==Construct the LC circuit using a non-polar capacitor== | ==Construct the LC circuit using a non-polar capacitor== | ||
Revision as of 20:53, 3 February 2011
- LC Resonance circuits
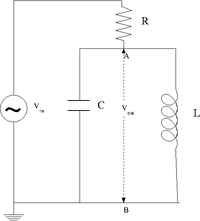
The LC circuit
Design a parallel LC resonant circuit with a resonant frequency between 50-200 kHz. use = 10 - 100 , R = 1k
I choose the following values for and :
So the resonance frequency is
Or
Let's estimate:
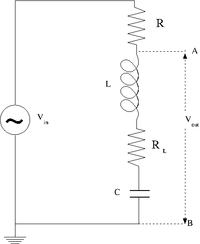
Construct the LC circuit using a non-polar capacitor
Measure the Gain as a function of frequency. (25 pnts)
Compare the measured and theoretical values of the resonance frequency () (10 pnts)
Questions
1.Is there a value of in which at resonance. What is the value?(5 pnts)