Difference between revisions of "Lab 5 RS"
Jump to navigation
Jump to search
| Line 9: | Line 9: | ||
:<math>\omega_0=\frac{1}{\sqrt{\mbox{LC}}}</math> | :<math>\omega_0=\frac{1}{\sqrt{\mbox{LC}}}</math> | ||
| − | I choose the following values for <math>\mbox{R | + | I choose the following values for <math>\mbox{R}</math> and <math>\mbox{C}</math>: |
| + | |||
| + | :<math>R=aaa\ \Omega</math> | ||
| + | :<math>C=bbb\ \pico F</math> | ||
| + | |||
| + | So the resonance frequency is <math>\omega_0=\frac{1}{\sqrt{aaa\ \Omega\ bbb\ \pico F }}</math> | ||
==Construct the LC circuit using a non-polar capacitor== | ==Construct the LC circuit using a non-polar capacitor== | ||
Revision as of 04:59, 1 February 2011
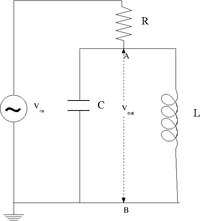
- LC Resonance circuits
The LC cicuit
Design a parallel LC resonant circuit with a resonant frequency between 50-200 kHz. use = 10 - 100 .
I choose the following values for and :
So the resonance frequency is
Construct the LC circuit using a non-polar capacitor
Measure the Gain as a function of frequency. (20 pnts)
Measure the Gain when an external resistance approximately equals to the inherent resistance of the rf choke . (20 pnts)
Compare the measured and theoretical values from the resonance frequency () and the Quality factor value for each case; . (10 pnts)
Questions
- If r=0, show that . (10 pnts)
- Show that at resonance. (10 pnts)
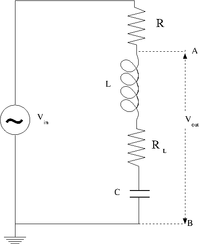
The LRC cicuit
- Design and construct a series LRC circuit.
- Measure and Graph the Gain as a function of the oscillating input voltage frequency. (20 pnts)
Questions
- What is the current at resonance? (5 pnts)
- What is the current as ? (5 pnts)