Difference between revisions of "Lab 3 RS"
| Line 105: | Line 105: | ||
At the break point the voltage gain is down by 3 dB relative to the gain of unity at zero frequency. So the value of <math>\mbox{log}(V_{out}/V_{in}) = (3/20) = 0.15 </math>. Using this value I found from plot above <math>\mbox{log}(f_b) = 1.1\ \mbox{kHz}</math>. So <math>f_b = (10^{1.1}) = 12.59\ \mbox{kHz}</math>. The error in this case is <math>3.79\ %</math> | At the break point the voltage gain is down by 3 dB relative to the gain of unity at zero frequency. So the value of <math>\mbox{log}(V_{out}/V_{in}) = (3/20) = 0.15 </math>. Using this value I found from plot above <math>\mbox{log}(f_b) = 1.1\ \mbox{kHz}</math>. So <math>f_b = (10^{1.1}) = 12.59\ \mbox{kHz}</math>. The error in this case is <math>3.79\ %</math> | ||
| − | ==Calculate and expression for <math>\frac{V_{out}}{ V_{in}}</math> as a function of <math>\nu</math>, <math>R</math>, and <math>C</math>. The Gain is defined as the ratio of <math>V_{out}</math> to <math>V_{in}</math>.(5 pnts)== | + | ==2. Calculate and expression for <math>\frac{V_{out}}{ V_{in}}</math> as a function of <math>\nu</math>, <math>R</math>, and <math>C</math>. The Gain is defined as the ratio of <math>V_{out}</math> to <math>V_{in}</math>.(5 pnts)== |
We have: | We have: | ||
| Line 123: | Line 123: | ||
:<math>\left |\frac{V_{out}}{V_{in}} \right | = \sqrt{ \left( \frac{V_{out}}{V_{in}} \right)^* \left( \frac{V_{out}}{V_{in}} \right)} = \sqrt{\left ( \frac{1}{1+i\omega RC}\right ) \left ( \frac{1}{1-i\omega RC}\right )} = \frac{1}{\sqrt{(1 + (\omega RC)^2}} = \frac{1}{\sqrt{(1 + (2\pi \nu RC)^2}}</math> | :<math>\left |\frac{V_{out}}{V_{in}} \right | = \sqrt{ \left( \frac{V_{out}}{V_{in}} \right)^* \left( \frac{V_{out}}{V_{in}} \right)} = \sqrt{\left ( \frac{1}{1+i\omega RC}\right ) \left ( \frac{1}{1-i\omega RC}\right )} = \frac{1}{\sqrt{(1 + (\omega RC)^2}} = \frac{1}{\sqrt{(1 + (2\pi \nu RC)^2}}</math> | ||
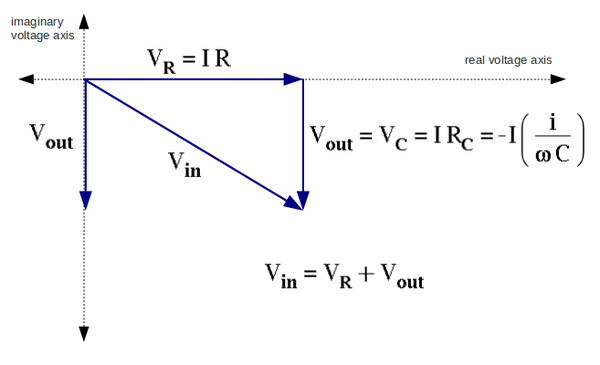
| − | ==Sketch the phasor diagram for <math>V_{in}</math>,<math> V_{out}</math>, <math>V_{R}</math>, and <math>V_{C}</math>. Put the current <math>I</math> along the real voltage axis. (30 pnts)== | + | ==3. Sketch the phasor diagram for <math>V_{in}</math>,<math> V_{out}</math>, <math>V_{R}</math>, and <math>V_{C}</math>. Put the current <math>I</math> along the real voltage axis. (30 pnts)== |
[[File:Phase diagram m.png | 600 px]] | [[File:Phase diagram m.png | 600 px]] | ||
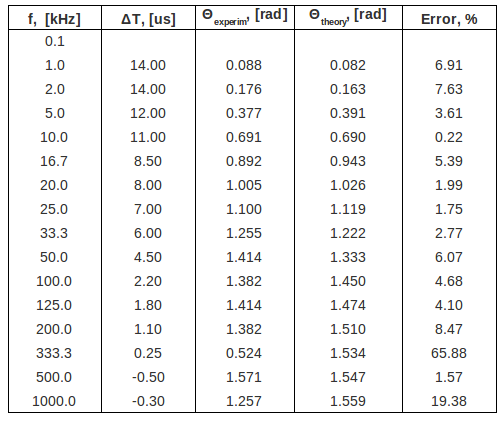
| − | ==Compare the theoretical and experimental value for the phase shift <math>\theta</math>. (5 pnts)== | + | ==4. Compare the theoretical and experimental value for the phase shift <math>\theta</math>. (5 pnts)== |
The experimental phase shift is <math>\ \Theta_{exper} = (-\omega\ \delta T)_{exper}</math> | The experimental phase shift is <math>\ \Theta_{exper} = (-\omega\ \delta T)_{exper}</math> | ||
| Line 136: | Line 136: | ||
[[File:Phase_table_m2.png | 600 px]] | [[File:Phase_table_m2.png | 600 px]] | ||
| − | ==What is the phase shift <math>\theta</math> for a DC input and a very-high frequency input?(5 pnts)== | + | ==5. What is the phase shift <math>\theta</math> for a DC input and a very-high frequency input?(5 pnts)== |
Because a DC circuit doesn't have any oscillation there are no any phase shift. | Because a DC circuit doesn't have any oscillation there are no any phase shift. | ||
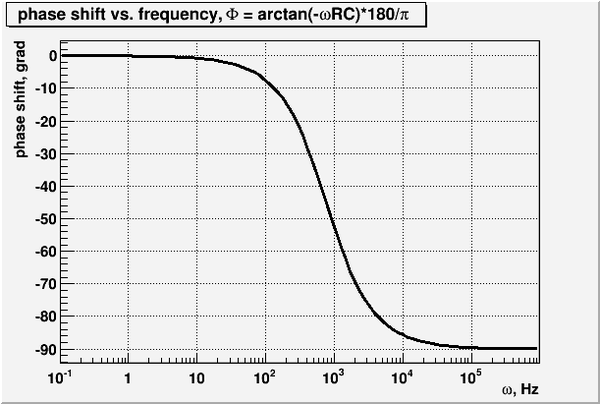
| − | ==Calculate and expression for the phase shift <math>\theta</math> as a function of <math>\nu</math>, <math>R</math>, <math>C</math> and graph <math>\theta</math> -vs <math>\nu</math>. (20 pnts)== | + | ==6. Calculate and expression for the phase shift <math>\theta</math> as a function of <math>\nu</math>, <math>R</math>, <math>C</math> and graph <math>\theta</math> -vs <math>\nu</math>. (20 pnts)== |
From the phasor diagram above (question 3) the angle between vectors <math>V_{in}</math> and <math>V_{out}</math> given by | From the phasor diagram above (question 3) the angle between vectors <math>V_{in}</math> and <math>V_{out}</math> given by | ||
Revision as of 07:01, 27 January 2011
- RC Low-pass filter
1-50 kHz filter (20 pnts)
1. Design a low-pass RC filter with a break point between 1-50 kHz. The break point is the frequency at which the filter starts to attenuate the AC signal. For a Low pass filter, AC signals with a frequency above 1-50 kHz will start to be attenuated (not passed)
- To design low-pass RC filter I had:
So
2. Now construct the circuit using a non-polar capacitor
3. Use a sinusoidal variable frequency oscillator to provide an input voltage to your filter
4. Measure the input and output voltages for at least 8 different frequencies which span the frequency range from 1 Hz to 1 MHz
| 0.1 | 5.0 | 5.0 | 1.0 |
| 1.0 | 4.2 | 4.2 | 1.0 |
| 2.0 | 3.2 | 3.1 | 0.97 |
| 5.0 | 1.8 | 1.6 | 0.89 |
| 10.0 | 1.14 | 0.88 | 0.77 |
| 16.7 | 0.90 | 0.54 | 0.60 |
| 20.0 | 0.88 | 0.48 | 0.54 |
| 25.0 | 0.82 | 0.38 | 0.46 |
| 33.3 | 0.78 | 0.28 | 0.36 |
| 50.0 | 0.76 | 0.18 | 0.24 |
| 100.0 | 0.75 | 0.09 | 0.12 |
| 125.0 | 0.74 | 0.07 | 0.095 |
| 200.0 | 0.75 | 0.04 | 0.053 |
| 333.3 | 0.76 | 0.03 | 0.039 |
| 200.0 | 0.76 | 0.03 | 0.039 |
| 1000.0 | 0.78 | 0.06 | 0.077 |
5. Graph the -vs-
phase shift (10 pnts)
- measure the phase shift between and as a function of frequency . Hint: you could use as an external trigger and measure the time until reaches a max on the scope .
See question 4 about my phase shift measurements
Questions
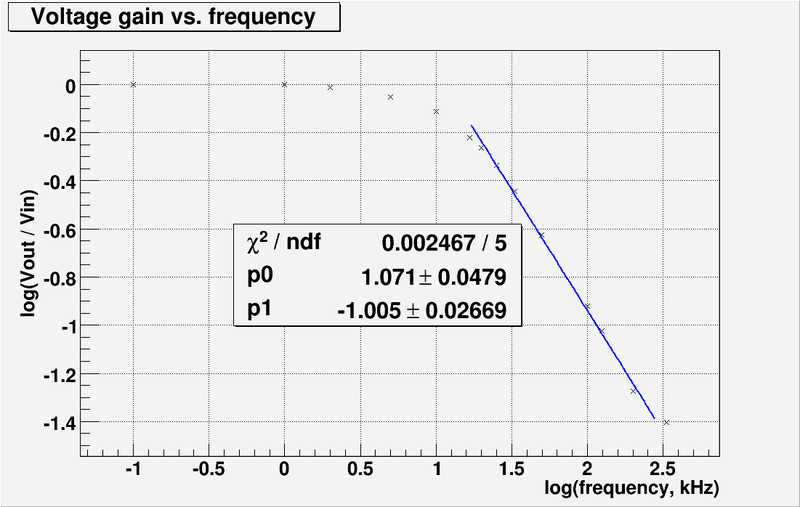
1. Compare the theoretical and experimentally measured break frequencies. (5 pnts)
method 1. Using fitting line
- Theoretical break frequency:
- Experimentally measured break frequency:
Q: The above was read off the graph? Why not use fit results? A: The fit was made by using GIMP Image Editor. I do not have so much experience with ROOT. But I will try to do it. Thank you for comment. A1: The fit was done by ROOT. The graph above was replaced.
- The fit line equation from the plot above is .
- From intersection point of line with x-axis we find:
- The error is:
method 2. Using the -3 dB point
At the break point the voltage gain is down by 3 dB relative to the gain of unity at zero frequency. So the value of . Using this value I found from plot above . So . The error in this case is
2. Calculate and expression for as a function of , , and . The Gain is defined as the ratio of to .(5 pnts)
We have:
Dividing second equation into first one we get the voltage gain:
And we are need the real part:
3. Sketch the phasor diagram for ,, , and . Put the current along the real voltage axis. (30 pnts)
4. Compare the theoretical and experimental value for the phase shift . (5 pnts)
The experimental phase shift is
The theoretical phase shift is
5. What is the phase shift for a DC input and a very-high frequency input?(5 pnts)
Because a DC circuit doesn't have any oscillation there are no any phase shift.
6. Calculate and expression for the phase shift as a function of , , and graph -vs . (20 pnts)
From the phasor diagram above (question 3) the angle between vectors and given by