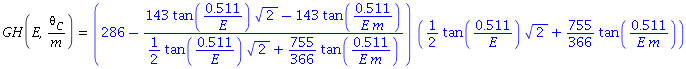Difference between revisions of "Minimum accelerator energy to run experiment"
| Line 9: | Line 9: | ||
I can express the distance <math>A_1D_1</math> as function of collimator size <math>\Theta_C/m</math> and electron beam energy E: | I can express the distance <math>A_1D_1</math> as function of collimator size <math>\Theta_C/m</math> and electron beam energy E: | ||
| − | <math>A_1D_1(E,\ \Theta_C/m) = \frac{469}{2}\tan\left(\frac{0.511}{E}\right) | + | <math>A_1D_1(E,\ \Theta_C/m) = \frac{469}{sqrt{2}}\tan\left(\frac{0.511}{E}\right) |
| − | + \frac{469} | + | + \frac{469}{2}\tan\left(\frac{1}{m}\frac{0.511}{E}\right)</math> |
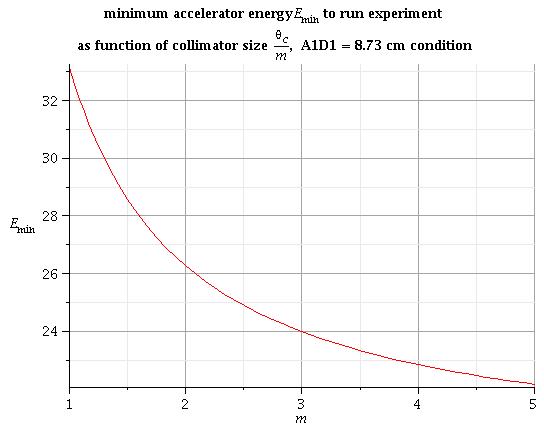
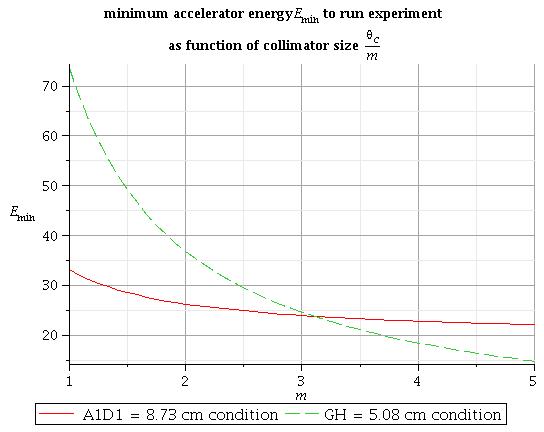
To fit the collimator size into the hole through the concrete wall with radius R = 8.73 cm we need to solve equation: | To fit the collimator size into the hole through the concrete wall with radius R = 8.73 cm we need to solve equation: | ||
Revision as of 22:44, 14 June 2010
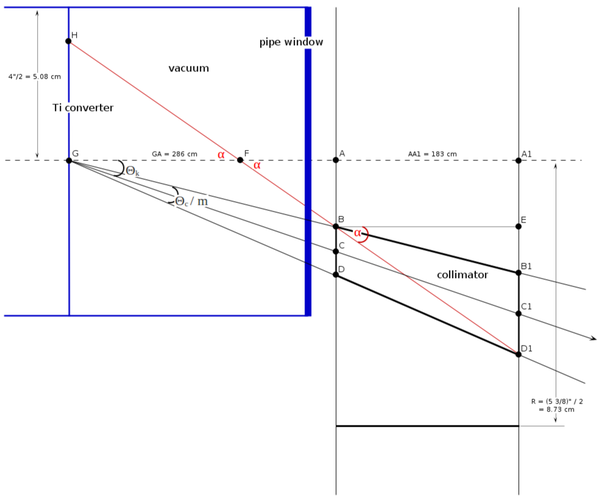
general setup
fitting the collimator size into the hole through the concrete wall
I can express the distance as function of collimator size and electron beam energy E:
To fit the collimator size into the hole through the concrete wall with radius R = 8.73 cm we need to solve equation:
1) some solutions of this equation for different collimator size m are:
2) in general for arbitrary collimator size m the solutions are:
All energy under this line is good to run experiment for condition above
nothing hitting the box going through the collimator condition
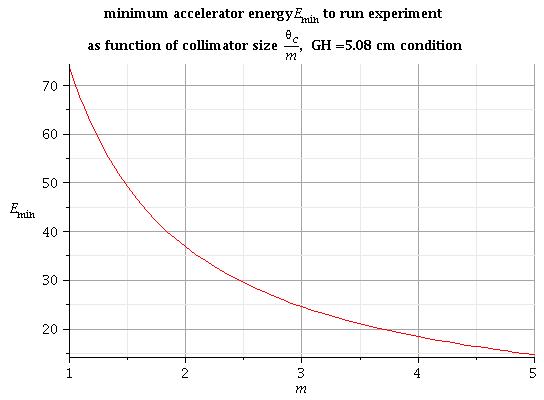
Also I can express the distance as function of collimator size and electron beam energy E:
If I would like that nothing hitting the 4" box to go through the collimator I need to solve equation:
1) some solutions of this equation for different collimator size m are:
2) in general for arbitrary collimator size m the solutions are:
All energy under this line is good to run experiment for condition above
both conditions above are together
All energy under this linse is good to run experiment for both conditions above