|
|
| Line 1: |
Line 1: |
| | [http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | | [http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] |
| | | | |
| − | =Minimum accelerator energy to run experiment=
| + | =condition 1: fitting the collimator size into the hole= |
| − | | |
| − | ==condition 1: fitting the collimator size into the hole==
| |
| − | | |
| − | [[File:min_energy.png|800px]]
| |
| − | | |
| − | The minimum energy of accelerator (MeV) is limited by fitting the collimator size <math>r_2</math> into the hole R = 8.73 cm:
| |
| − | | |
| − | <math>x_2 + r_2 = R</math>
| |
| − | | |
| − | 1) Assuming the collimator diameter is <math>\Theta_C</math>:
| |
| − | | |
| − | <math>\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
| |
| − | \frac{1}{2}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 33.1\ MeV </math>
| |
| − | | |
| − | 2) Assuming the collimator diameter is <math>\Theta_C/2</math>:
| |
| − | | |
| − | <math>\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
| |
| − | \frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{2}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 26.3\ MeV </math>
| |
| − | | |
| − | 3) Assuming the collimator diameter is <math>\Theta_C/4</math>:
| |
| − | | |
| − | <math>\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
| |
| − | \frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{4}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 22.8\ MeV </math>
| |
| − | | |
| − | 4) for arbitrary collimator size <math>\Theta_C/2</math>:
| |
| − | | |
| − | [[File:plot_energy_collimatorsize.jpeg]]
| |
| − | | |
| − | All energy above this line is good to run experiment
| |
| − | | |
| − | ==condition 2: F1A = 286 cm==
| |
| − | | |
| − | 1) assuming the collimator diameter is <math>\Theta_C</math>
| |
| − | | |
| − | <math> E_{min} = 73.7\ MeV </math>
| |
| − | | |
| − | 2) assuming the collimator diameter is <math>\Theta_C/2</math>
| |
| − | | |
| − | <math> E_{min} = 36.9\ MeV </math>
| |
| − | | |
| − | 3) assuming the collimator diameter is <math>\Theta_C/4</math>
| |
| − | | |
| − | <math> E_{min} = 18.4\ MeV </math>
| |
| − | | |
| − | 4) for arbitrary collimator size <math>\Theta_C/m</math>:
| |
| − | | |
| − | [[File:plot_energy_F1A.jpeg]]
| |
| − | | |
| − | All energy above this line is good to run experiment
| |
| − | | |
| − | ==both conditions above are together==
| |
| − | | |
| − | [[File:plot_energy_bothcondition.jpeg]]
| |
| − | | |
| − | All energy above this lines is good to run experiment
| |
| − | | |
| − | [http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back]
| |
| − | | |
| − | =Minimum accelerator energy to run experiment=
| |
| − | | |
| − | ==condition 1: fitting the collimator size into the hole==
| |
| | | | |
| | [[File:min_energy.png|800px]] | | [[File:min_energy.png|800px]] |
| Line 91: |
Line 30: |
| | All energy above this line is good to run experiment | | All energy above this line is good to run experiment |
| | | | |
| − | ==condition 2: F1A = 286 cm==
| + | =condition 2: F1A = 286 cm= |
| | | | |
| | 1) assuming the collimator diameter is <math>\Theta_C</math> | | 1) assuming the collimator diameter is <math>\Theta_C</math> |
| Line 111: |
Line 50: |
| | All energy above this line is good to run experiment | | All energy above this line is good to run experiment |
| | | | |
| − | ==both conditions above are together==
| + | =both conditions above are together= |
| | | | |
| | [[File:plot_energy_bothcondition.jpeg]] | | [[File:plot_energy_bothcondition.jpeg]] |
Go Back
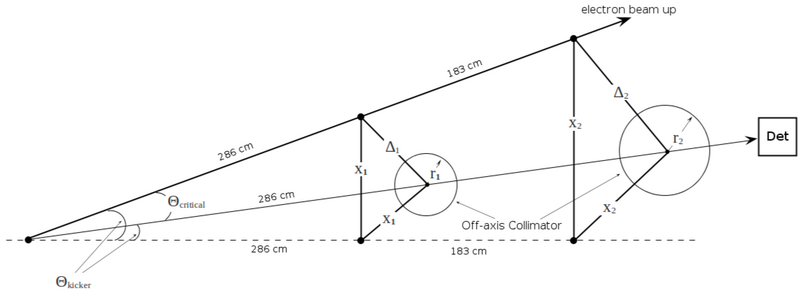
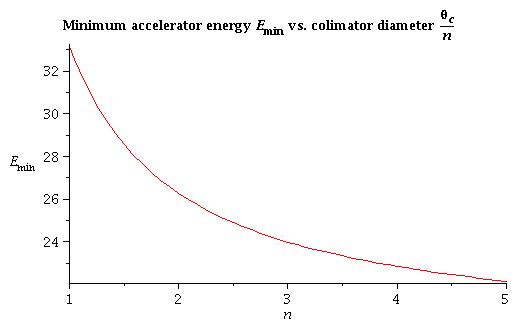
condition 1: fitting the collimator size into the hole
The minimum energy of accelerator (MeV) is limited by fitting the collimator size [math]r_2[/math] into the hole R = 8.73 cm:
[math]x_2 + r_2 = R[/math]
1) Assuming the collimator diameter is [math]\Theta_C[/math]:
[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
\frac{1}{2}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 33.1\ MeV [/math]
2) Assuming the collimator diameter is [math]\Theta_C/2[/math]:
[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
\frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{2}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 26.3\ MeV [/math]
3) Assuming the collimator diameter is [math]\Theta_C/4[/math]:
[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
\frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{4}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 22.8\ MeV [/math]
4) for arbitrary collimator size [math]\Theta_C/2[/math]:
All energy above this line is good to run experiment
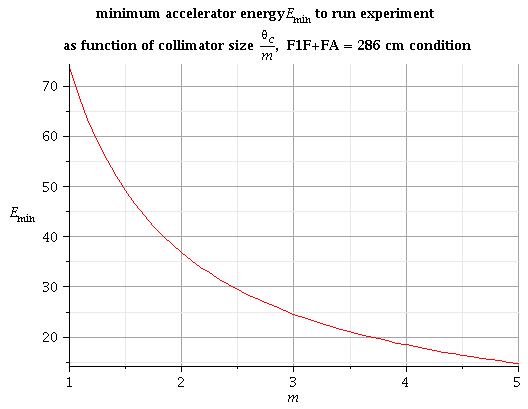
condition 2: F1A = 286 cm
1) assuming the collimator diameter is [math]\Theta_C[/math]
[math] E_{min} = 73.7\ MeV [/math]
2) assuming the collimator diameter is [math]\Theta_C/2[/math]
[math] E_{min} = 36.9\ MeV [/math]
3) assuming the collimator diameter is [math]\Theta_C/4[/math]
[math] E_{min} = 18.4\ MeV [/math]
4) for arbitrary collimator size [math]\Theta_C/m[/math]:
All energy above this line is good to run experiment
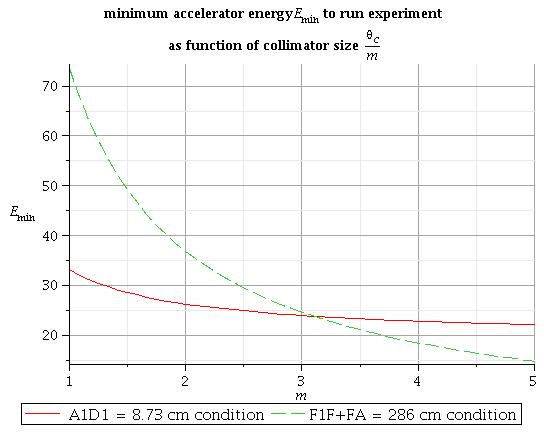
both conditions above are together
All energy above this lines is good to run experiment
Go Back
