|
|
| Line 30: |
Line 30: |
| | =25 MeV geometry= | | =25 MeV geometry= |
| | | | |
| | + | ==geometry calculation== |
| | | | |
| | {| border="1" cellpadding="20" cellspacing="0" | | {| border="1" cellpadding="20" cellspacing="0" |
| Line 48: |
Line 49: |
| | |} | | |} |
| | | | |
| − | | + | ==geometry pictures== |
| − | ==critical angle==
| |
| − | | |
| − | <math>\Theta_C = \frac{m_ec^2}{E_{beam}} = \frac{0.511\ MeV}{25\ MeV} = 1.17\ ^o</math><br>
| |
| − | | |
| − | ==kicker angle==
| |
| − | | |
| − | <math>\Delta_1 = 286\ cm\ *\ \tan(1.17^o) = 5.84\ cm</math> <br>
| |
| − | <math>x^2+x^2 = 5.84^2\ cm \ \ \Rightarrow\ \ x = 4.13\ cm
| |
| − | \Rightarrow\ \ \tan^{-1}\left(\frac{4.13}{286}\right) = 0.827\ ^o</math><br>
| |
| − | | |
| − | ==geometry (<math> \Theta_c/2</math>)== | |
| − | | |
| − | ===collimator center position===
| |
| − | | |
| − | <math>286\ cm \cdot \tan (0.827) = 4.13\ cm</math> (wall 1)<br>
| |
| − | <math>(286 + 183)\ cm \cdot \tan (0.827) = 6.77\ cm</math> (wall 2)
| |
| − | | |
| − | ===collimator diameter===
| |
| − |
| |
| − | <math>286\ cm \cdot \tan (1.17/2) = 2.92\ cm</math> (wall 1)<br>
| |
| − | <math>(286 + 183)\ cm \cdot \tan (1.17/2) = 4.79\ cm</math> (wall 2)
| |
| − | | |
| − | ===collimator critical angle===
| |
| − | | |
| − | <math> AB = AC - BD/2 = (4.13 - 2.92/2)\ cm = 2.67\ cm </math><br>
| |
| − | <math> A_1D_1 = A_1C_1 + B_1D_1/2 = (6.77 + 4.79/2)\ cm = 9.165\ cm </math><br>
| |
| − | <math>\bigtriangleup BED_1 \Rightarrow \tan (\alpha) = \frac{(9.165 - 2.67)\ cm}{183\ cm} \Rightarrow \alpha = 2.033^o</math>:
| |
| − | | |
| − | ===minimal distance from the wall (<math> \Theta_c/2</math>)===
| |
| − | | |
| − | <math>\bigtriangleup FAB \Rightarrow FA = \frac{AB}{\tan (2.033^o)} = \frac{2.67\ cm}{\tan (2.033^o)} = 75\ cm </math>
| |
| − | | |
| − | ==geometry (<math> \Theta_c/4</math>)==
| |
| − | | |
| − | ===collimator center position===
| |
| − | | |
| − | <math>286\ cm \cdot \tan (0.827) = 4.13\ cm</math> (wall 1)<br>
| |
| − | <math>(286 + 183)\ cm \cdot \tan (0.827) = 6.77\ cm</math> (wall 2)
| |
| − | | |
| − | ===collimator diameter===
| |
| − |
| |
| − | <math>286\ cm \cdot \tan (1.17/4) = 1.46\ cm</math> (wall 1)<br>
| |
| − | <math>(286 + 183)\ cm \cdot \tan (1.17/4) = 2.39\ cm</math> (wall 2)
| |
| − | | |
| − | ===collimator critical angle===
| |
| − | | |
| − | <math> AB = AC - BD/2 = (4.13 - 1.46/2)\ cm = 3.4\ cm </math><br>
| |
| − | <math> A_1D_1 = A_1C_1 + B_1D_1/2 = (6.77 + 2.39/2)\ cm = 7.965\ cm </math><br>
| |
| − | <math>\bigtriangleup BED_1 \Rightarrow \tan (\alpha) = \frac{(7.965 - 3.4)\ cm}{183\ cm} \Rightarrow \alpha = 1.429^o</math>:
| |
| − | | |
| − | ===minimal distance from the wall (<math> \Theta_c/4</math>)===
| |
| − | | |
| − | <math>\bigtriangleup FAB \Rightarrow FA = \frac{AB}{\tan (1.429^o)} = \frac{3.4\ cm}{\tan (1.429^o)} = 136\ cm </math>
| |
| − | | |
| − | ==Funny pictures...==
| |
| | | | |
| | ===how it looks 1 (<math> \Theta_c/2</math>, box 3"x4" and then pipe 4")=== | | ===how it looks 1 (<math> \Theta_c/2</math>, box 3"x4" and then pipe 4")=== |
Go Back
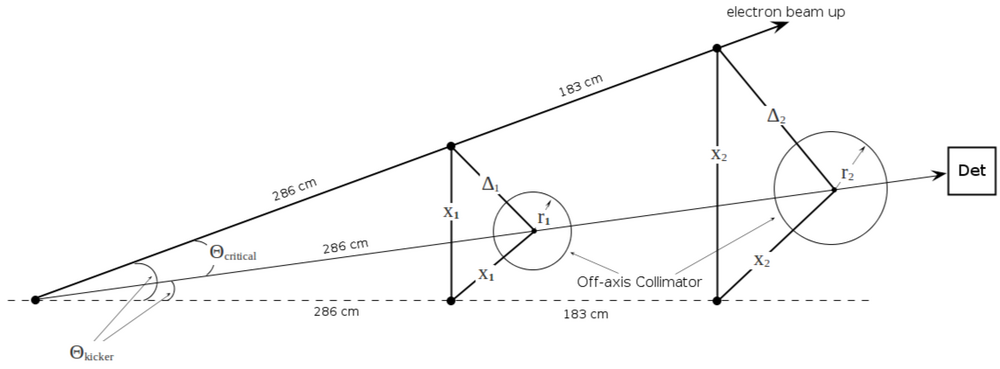
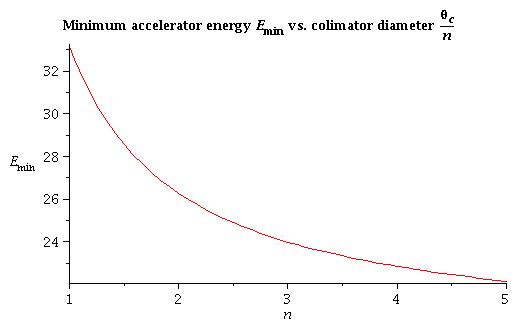
Minimum accelerator energy to run experiment
The minimum energy of accelerator (MeV) is limited by fitting the collimator ([math]r_2[/math]) into the hole ([math]R = 8.73\ cm[/math])
[math]x_2 + r_2 = R[/math]
1) Assuming the collimator diameter is [math]\Theta_C[/math]:
[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
\frac{1}{2}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 33.1\ MeV [/math]
2) Assuming the collimator diameter is [math]\Theta_C/2[/math]:
[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
\frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{2}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 26.3\ MeV [/math]
3) Assuming the collimator diameter is [math]\Theta_C/4[/math]:
[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
\frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{4}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 22.8\ MeV [/math]
4) In general:
25 MeV geometry
geometry calculation
| collimator diameter
|
[math]\Theta_{critical}[/math]
|
[math]\Theta_{kicker}[/math]
|
[math]\alpha_{collimator}[/math]
|
[math]AC[/math]
|
[math]A_1C_1[/math]
|
[math]BD[/math]
|
[math]B_1D_1[/math]
|
| [math]\frac{\Theta_{critical}}{2}[/math] |
[math]1.17^o[/math] |
[math]0.83^o[/math] |
[math]2.03^o[/math] |
4.13 |
6.78 |
2.92 |
4.79
|
| [math]\frac{\Theta_{critical}}{4}[/math] |
[math]1.17^o[/math] |
[math]0.82^o[/math] |
[math]1.43^o[/math] |
4.13 |
6.78 |
1.46 |
2.40
|
geometry pictures
how it looks 1 ([math] \Theta_c/2[/math], box 3"x4" and then pipe 4")
File:Vacuum pipe collimator .png
how it looks 2 ([math] \Theta_c/4[/math], box 3"x4" and then pipe 4")
File:Vacuum pipe collimator .png
Go Back
