Difference between revisions of "Geometry (25 MeV LINAC exit port)"
Jump to navigation
Jump to search
| Line 2: | Line 2: | ||
| − | =Critical angle | + | =Critical angle= |
| − | <math>\Theta = \frac{m_ec^2}{E_{beam}} = \frac{0.511\ MeV}{25\ MeV} = | + | <math>\Theta = \frac{m_ec^2}{E_{beam}} = \frac{0.511\ MeV}{25\ MeV} = 1.17\ ^o</math><br> |
| − | =Kicker angle and | + | =Kicker angle and displacements on the wall= |
| + | |||
| + | ==1 foot = 30.48 cm== | ||
==accelerator's side wall== | ==accelerator's side wall== | ||
| − | <math>\Delta = 286\ cm\ *\ \tan( | + | <math>\Delta = 286\ cm\ *\ \tan(1.17^o) = 5.84\ cm</math> |
| − | <math>x^2+x^2 = | + | <math>x^2+x^2 = 5.84^2\ cm \ \ \Rightarrow\ \ x = 4.13\ cm</math> |
| − | <math>\Delta = | + | <math>\Delta = 4.13\ cm \ \ \Rightarrow\ \ \tan^{-1}\left(\frac{2.36}{286}\right) = 0.47\ ^o</math> |
==detector's side wall== | ==detector's side wall== | ||
Revision as of 05:11, 11 June 2010
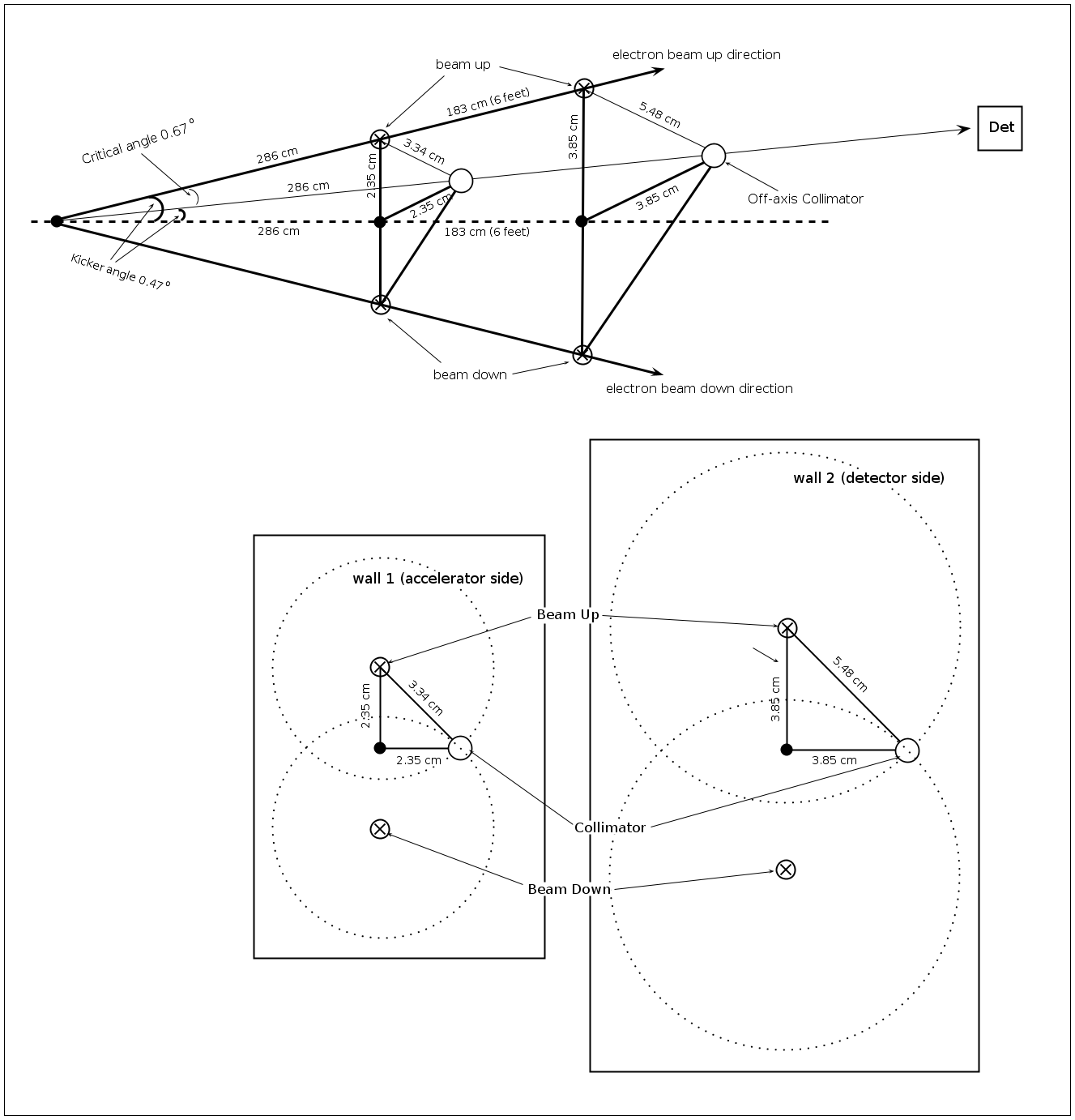
Critical angle
Kicker angle and displacements on the wall
1 foot = 30.48 cm
accelerator's side wall
detector's side wall
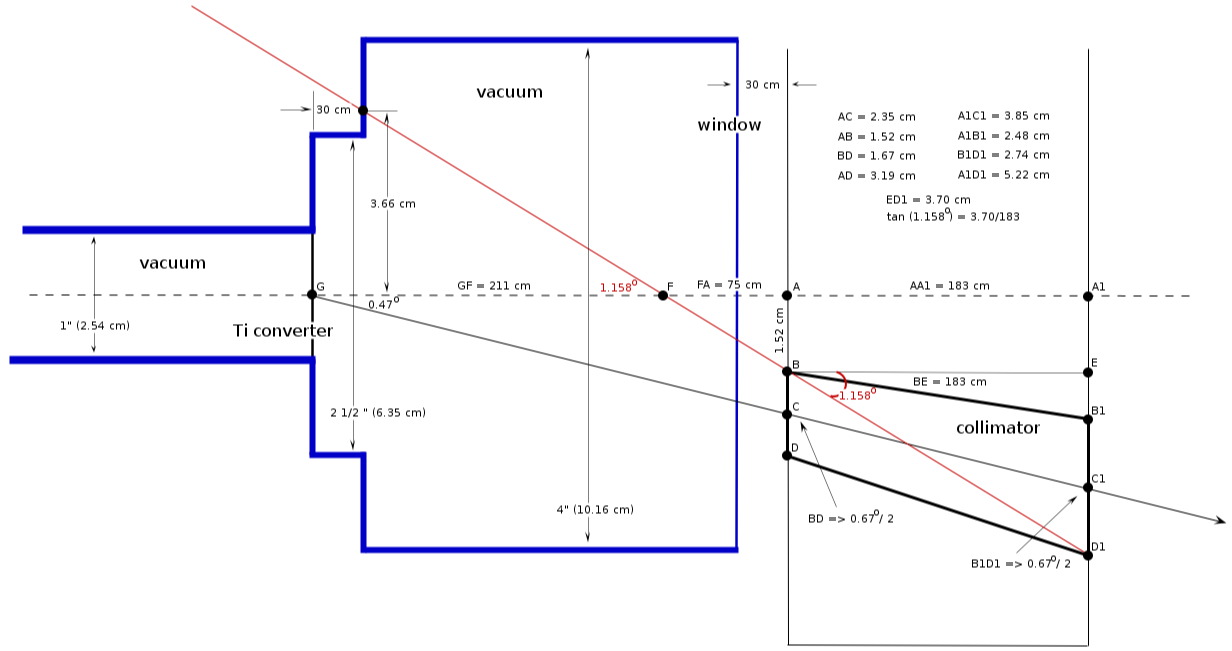
Off-axis collimation geometry
Vacuum pipe location ()
collimator location
1) center position:
(wall 1)
(wall 2)
2) collimator diameter:
(wall 1)
(wall 2)
collimator critical angle
from triangle :
minimal distance from the wall
from triangle FAB:
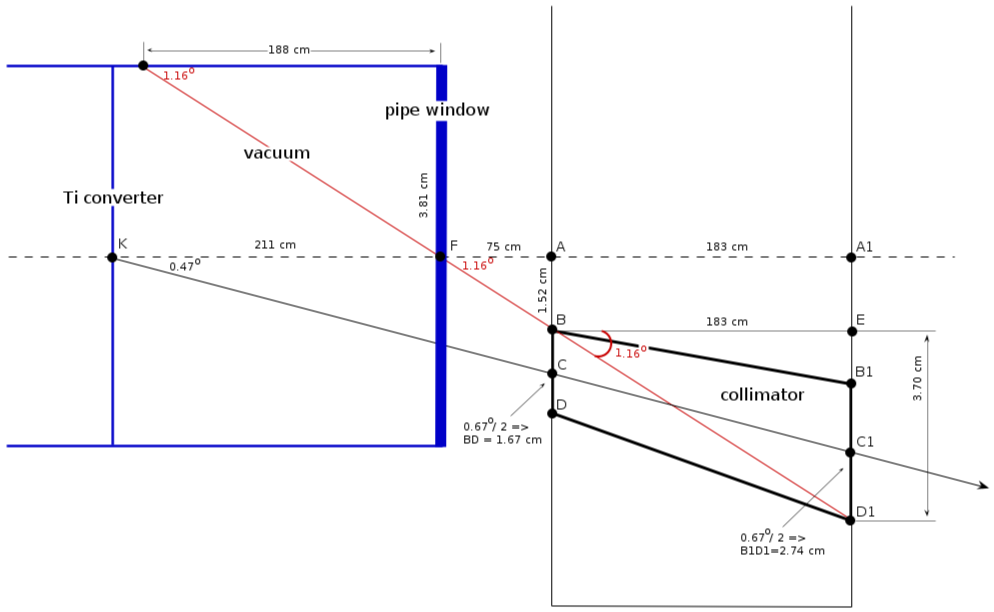
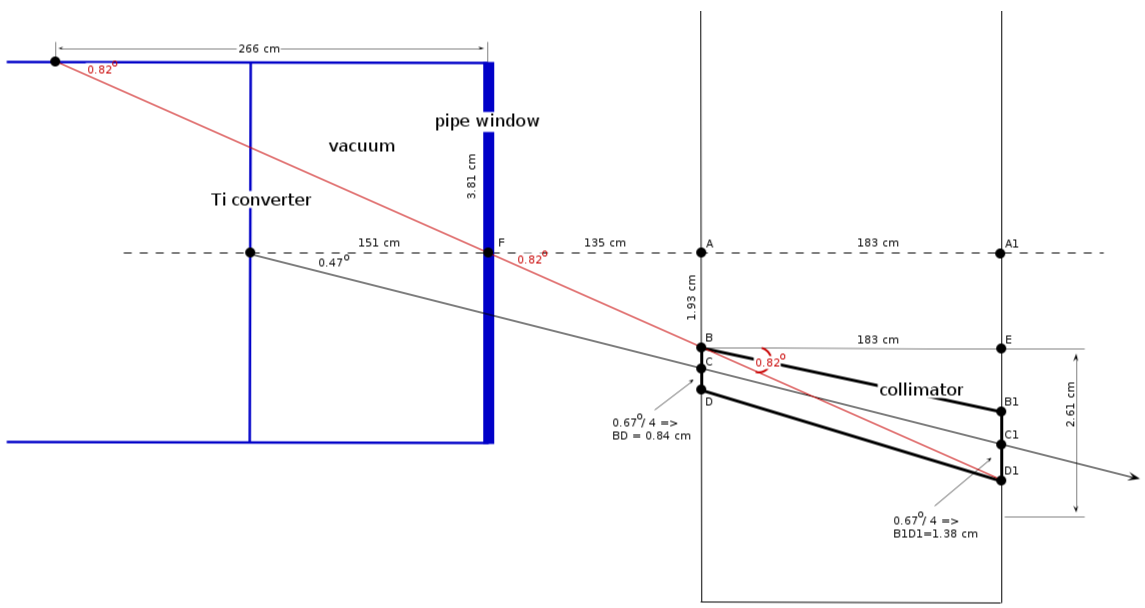
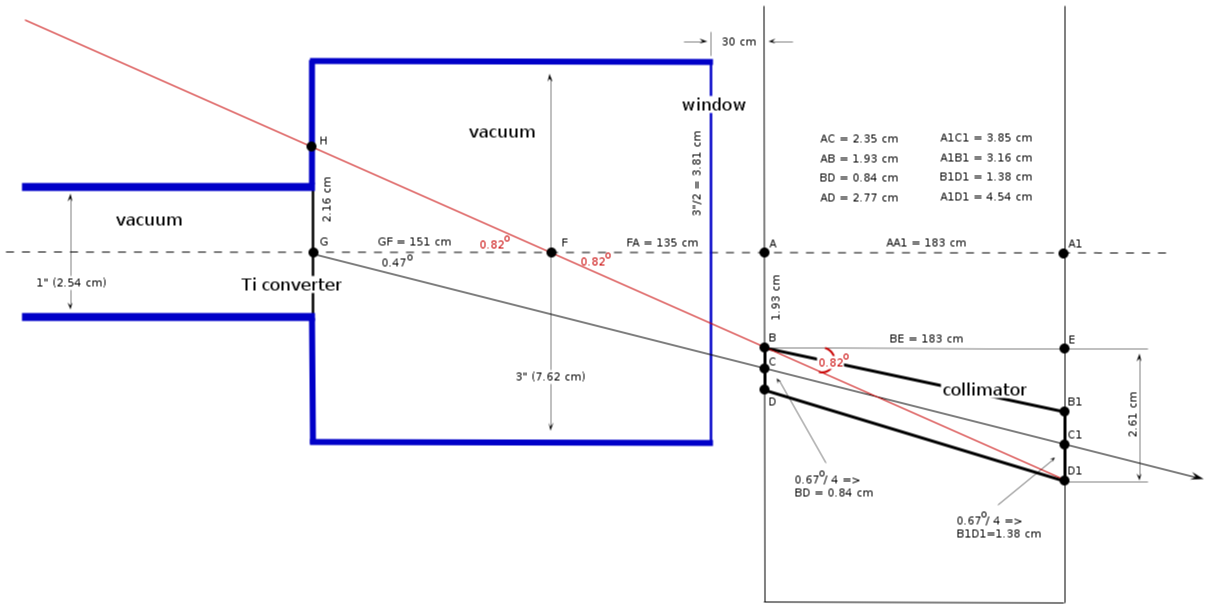
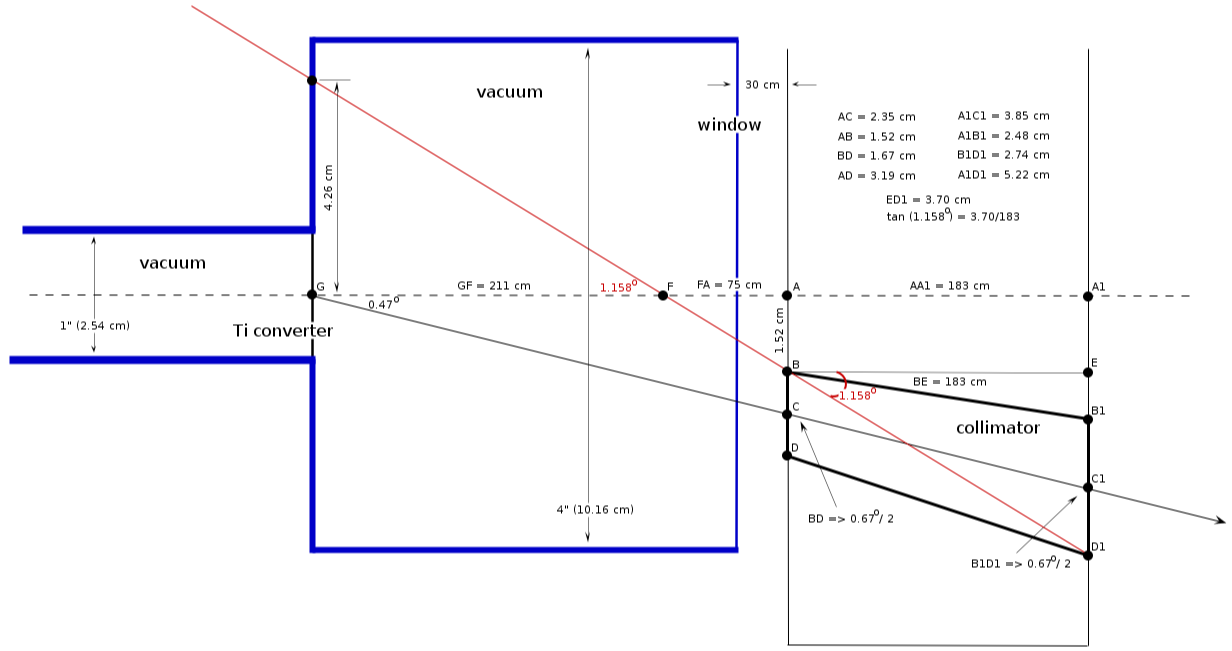
Vacuum pipe location ()
collimator location
1) center position:
(wall 1)
(wall 2)
2) collimator diameter:
(wall 1)
(wall 2)
collimator critical angle
from triangle :
minimal distance from the wall
from triangle FAB:
Funny pictures...
how it looks (, pipe 3")
how it looks 1 (, pipe 3")
how it looks 2 (, pipe 3")
how it looks 4 (, pipe (2 1/2)" and then pipe 4")
need to adjust to converter position
how it looks 5 (, box 3"x4" and then pipe 4")
need to adjust to converter position