Difference between revisions of "Geometry (44 MeV LINAC exit port)"
Jump to navigation
Jump to search
| Line 9: | Line 9: | ||
[[File:Beam_up_down.png]]<br> | [[File:Beam_up_down.png]]<br> | ||
| − | ==Critical and Kicker | + | ==Critical and Kicker angles== |
<math>\Theta_C = \frac{m_ec^2}{E}</math> | <math>\Theta_C = \frac{m_ec^2}{E}</math> | ||
| Line 17: | Line 17: | ||
= tan^-1\left(\frac{1}{\sqrt{2}}\ tan(\Theta_C)\right)</math><br> | = tan^-1\left(\frac{1}{\sqrt{2}}\ tan(\Theta_C)\right)</math><br> | ||
| − | == | + | ==Collimator location== |
| − | <math>\Delta_1 = 286\ cm\ \tan(\Theta_C) | + | <math>\Delta_1 = 286\ cm\ \tan(\Theta_C)<br> |
| − | <math> | + | <math>\Delta_2 = (286 + 183)\ cm\ \tan(\Theta_C)<br> |
| − | |||
| − | <math> | + | <math>x_1 = 286\ cm \ \tan(\Theta_K)</math><br> |
| − | <math> | + | <math>x_1 = (286 +183)\ cm \ \tan(\Theta_K)</math><br> |
| + | |||
| + | ==Collimator critical angle== | ||
| + | |||
| + | <math>\alpha = </math> | ||
=Vacuum pipe location (<math> \Theta_c/2</math>)= | =Vacuum pipe location (<math> \Theta_c/2</math>)= | ||
Revision as of 22:18, 20 June 2010
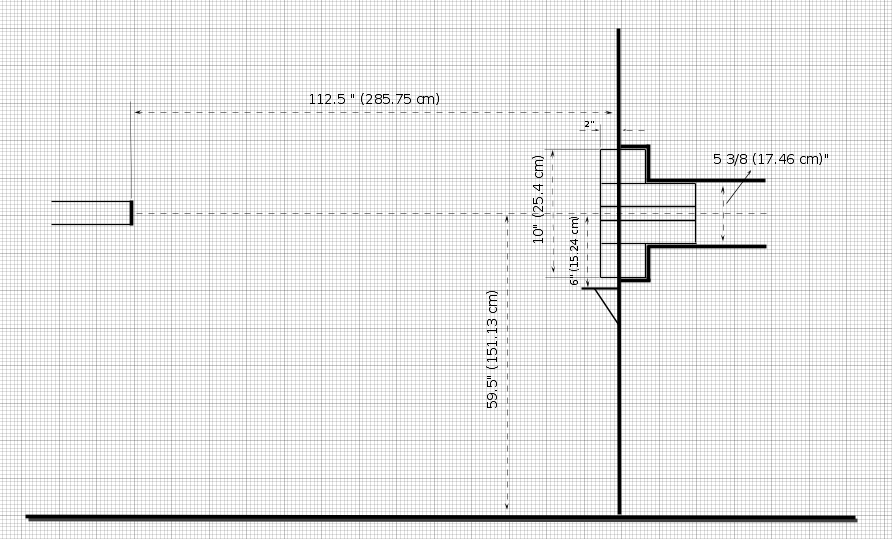
90 exit port geometry
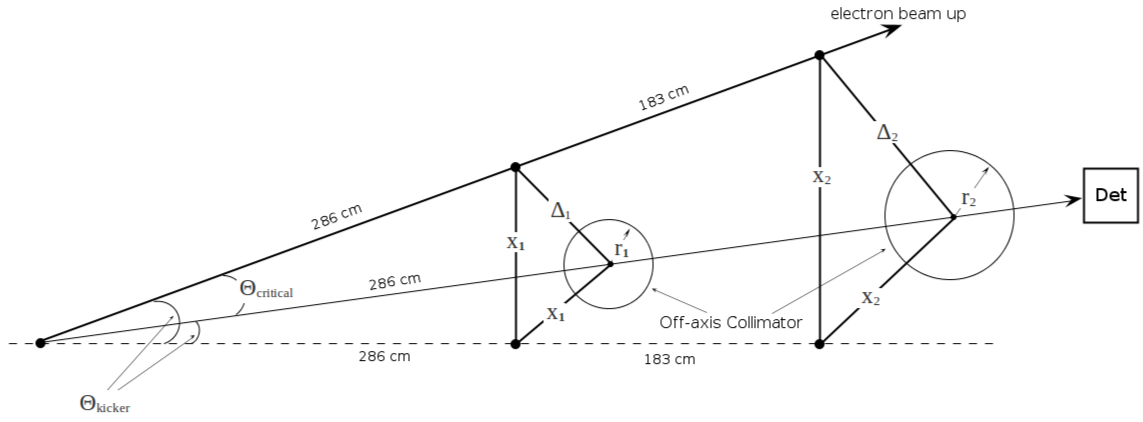
Off-axis collimation geometry
Critical and Kicker angles
Collimator location
Collimator critical angle
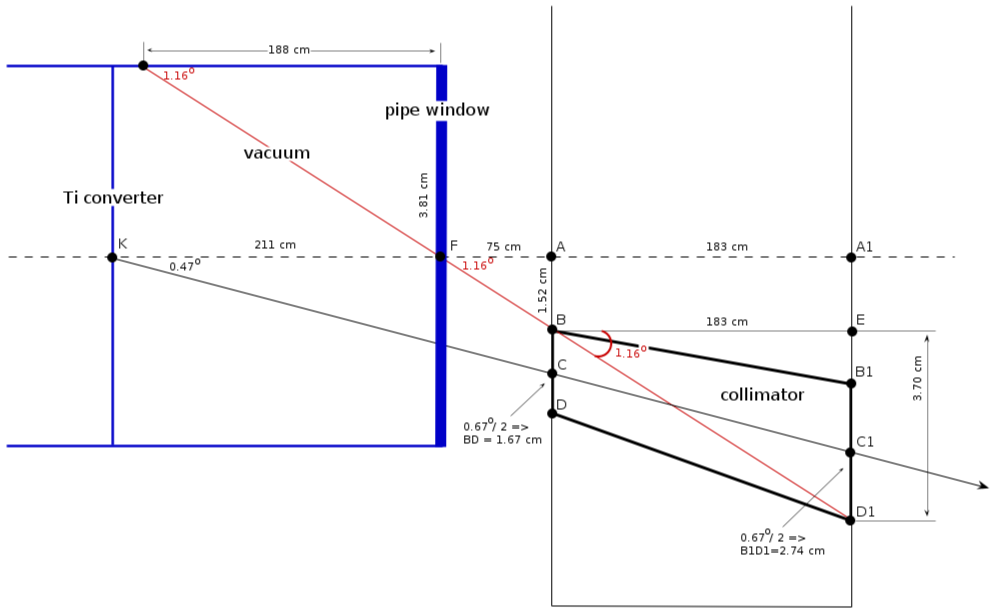
Vacuum pipe location ()
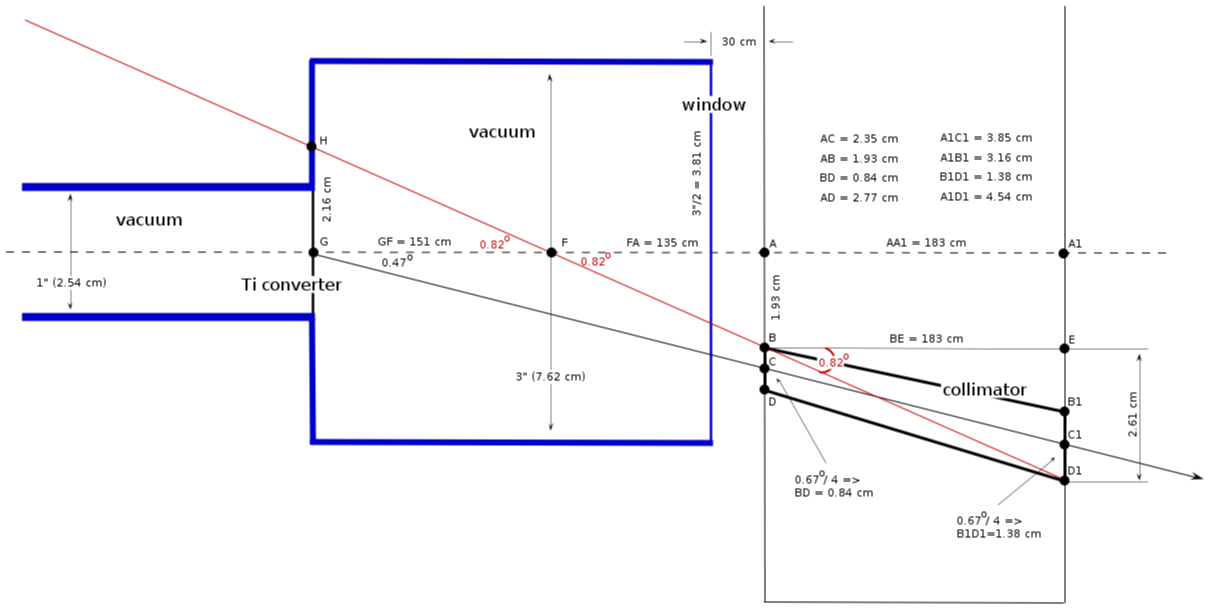
collimator location
1) center position:
(wall 1)
(wall 2)
2) collimator diameter:
(wall 1)
(wall 2)
collimator critical angle
from triangle :
minimal distance from the wall
from triangle FAB:
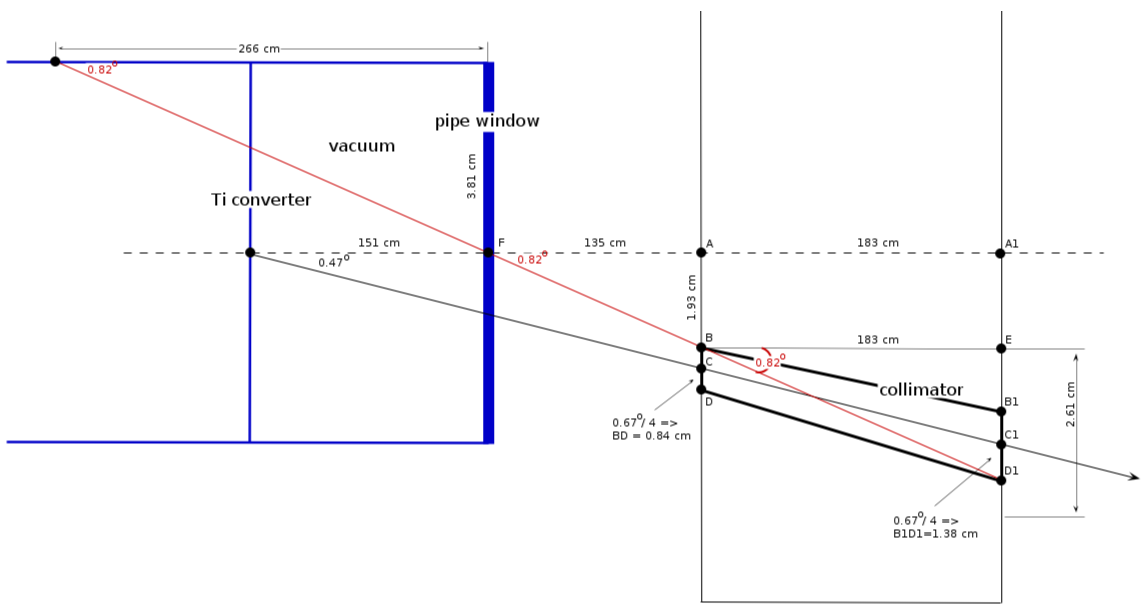
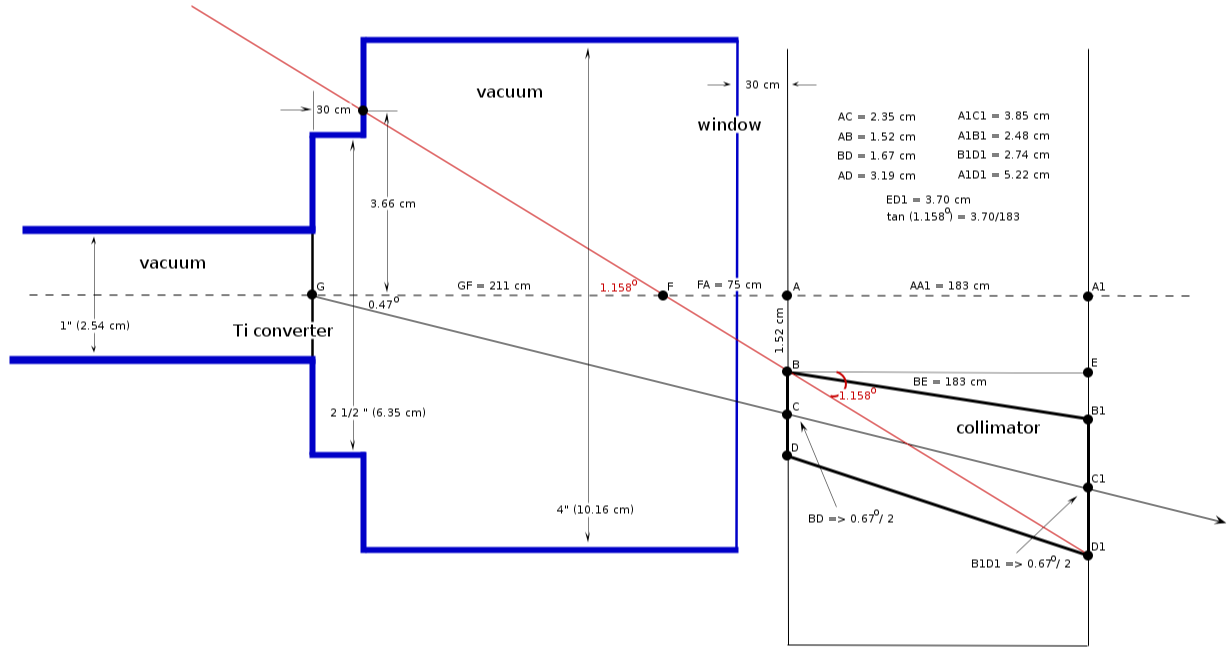
Vacuum pipe location ()
collimator location
1) center position:
(wall 1)
(wall 2)
2) collimator diameter:
(wall 1)
(wall 2)
collimator critical angle
from triangle :
minimal distance from the wall
from triangle FAB:
Funny pictures...
how it looks (, pipe 3")
how it looks 1 (, pipe 3")
how it looks 2 (, pipe 3")
how it looks 4 (, pipe (2 1/2)" and then pipe 4")
need to adjust to converter position
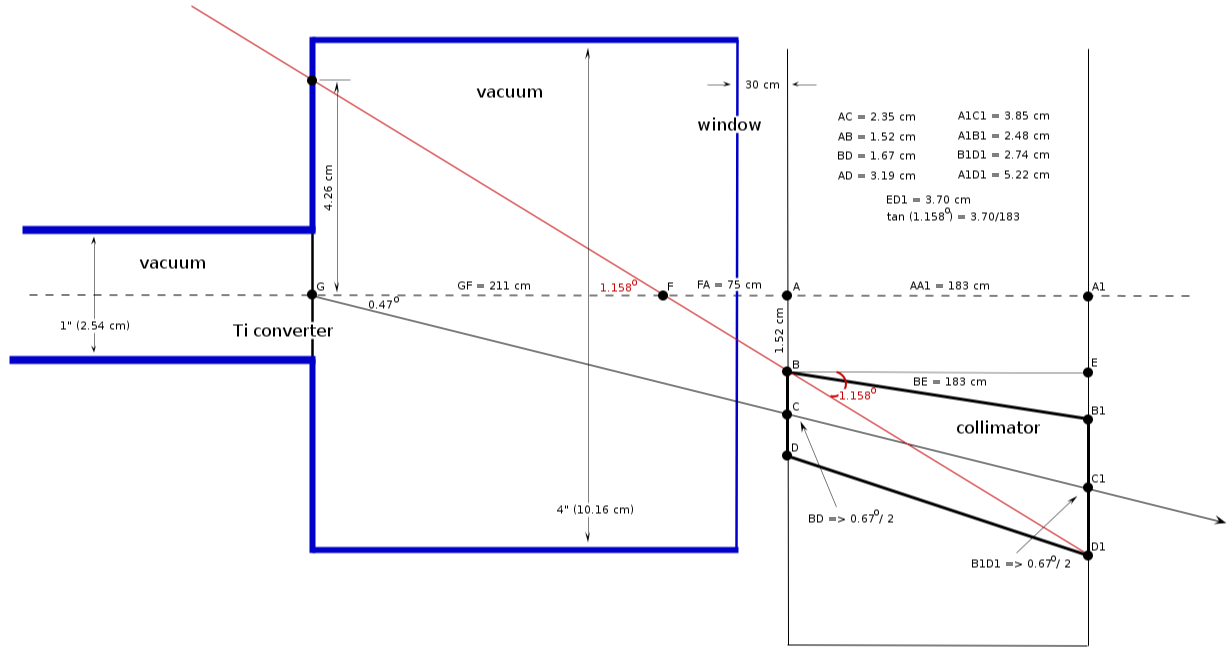
how it looks 5 (, box 3"x4" and then pipe 4")
need to adjust to converter position