Difference between revisions of "FC Analysis"
Jump to navigation
Jump to search
| (7 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
For each ADC channel: | For each ADC channel: | ||
<math> ADCSum^{channel}=\sum_{i=1}^{pulses}{ADC_{pulse}^{channel}}</math><br> | <math> ADCSum^{channel}=\sum_{i=1}^{pulses}{ADC_{pulse}^{channel}}</math><br> | ||
| − | <math> ADCErr^{channel}=\sqrt{\frac{\sum_{i=1}^{pulses}{ADC_{pulse}^{channel}}}{pulses}}</math> | + | <math> ADCErr^{channel}=\sqrt{\frac{\sum_{i=1}^{pulses}{ADC_{pulse}^{channel}}}{pulses}}</math><br> |
For distribution over all ADC channel: | For distribution over all ADC channel: | ||
<math> ADC^{avg}=\frac{\sum_{i=1}^{16}{ADCSum^{channel}*i}}{\sum_{i=1}^{16}{ADC_{i}}}</math><br> | <math> ADC^{avg}=\frac{\sum_{i=1}^{16}{ADCSum^{channel}*i}}{\sum_{i=1}^{16}{ADC_{i}}}</math><br> | ||
| − | <math> ADC^{err}=\frac{\sum_{i=1}^{16}{ADCErr^{channel}*i}}{\sum_{i=1}^{16}{ADC_{i}}}</math> | + | <math> ADC^{err}=\frac{\sum_{i=1}^{16}{ADCErr^{channel}*i}}{\sum_{i=1}^{16}{ADC_{i}}}</math><br> |
| − | |||
| Line 34: | Line 33: | ||
[[File:1461_1.png]][[File:1465_1.png]]<br><br> | [[File:1461_1.png]][[File:1465_1.png]]<br><br> | ||
| + | =3D Faraday cup plot= | ||
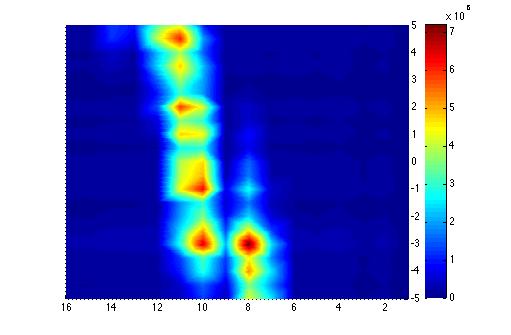
Below is the plot of the charge in Faraday cup (pC) as a function of magnet current (vertical axis, A) (basically magnetic field) and ADC (horizontal axis). | Below is the plot of the charge in Faraday cup (pC) as a function of magnet current (vertical axis, A) (basically magnetic field) and ADC (horizontal axis). | ||
[[File:Far.jpg]] | [[File:Far.jpg]] | ||
| + | |||
| + | =Faraday cup ADC channel distribution= | ||
| + | =Faraday cup rain= | ||
| + | |||
[http://wiki.iac.isu.edu/index.php/FC_Analysis Go Up] | [http://wiki.iac.isu.edu/index.php/FC_Analysis Go Up] | ||
Latest revision as of 03:57, 5 April 2010
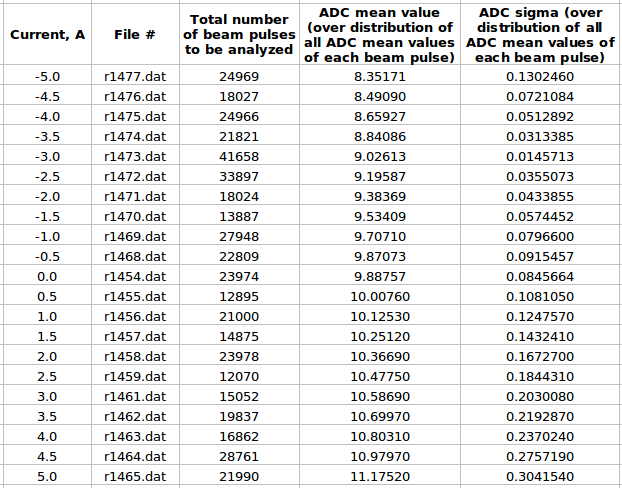
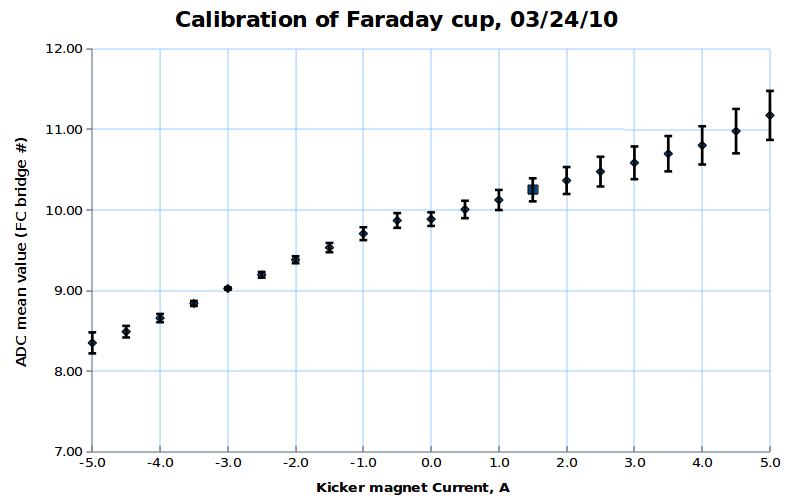
FC analysis using ADC channel current distribution
For each ADC channel:
For distribution over all ADC channel:
FC analysis using pulse by pulse ADC channel mean value distribution
For each beam pulse:
For distribution over all beam pulses:
Here is:
1. ADC# = bridge#
2. Pulse# = ReadOut# = Entry# = Event#
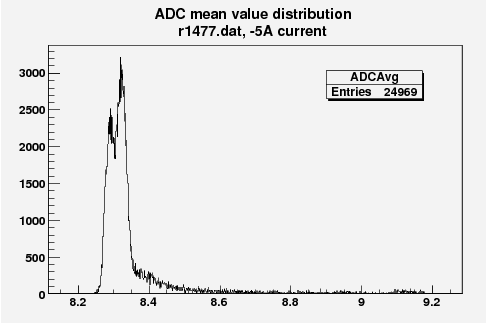
Some examples of ADC mean value distribution. Here are:
1. x axis: ADC mean value for one pulse
2. y axis: number of pulse w/ that ADC mean value
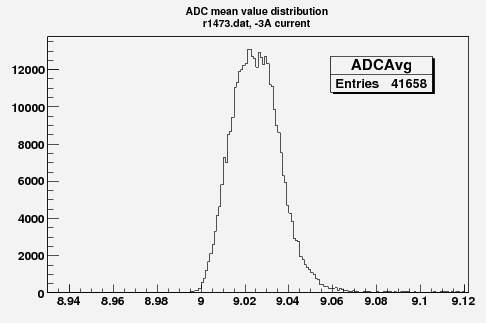
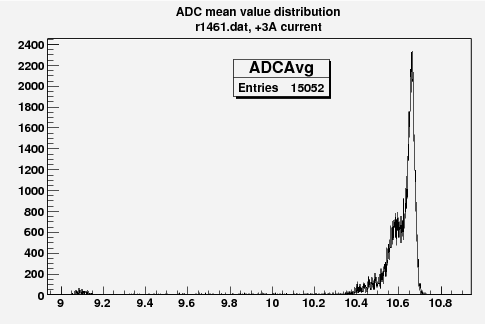
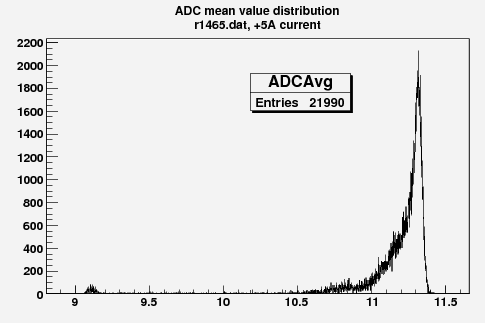
3D Faraday cup plot
Below is the plot of the charge in Faraday cup (pC) as a function of magnet current (vertical axis, A) (basically magnetic field) and ADC (horizontal axis).