Difference between revisions of "FC Analysis"
Jump to navigation
Jump to search
| Line 2: | Line 2: | ||
=FC analysis using ADC channel current distribution= | =FC analysis using ADC channel current distribution= | ||
| − | + | For each ADC channel: | |
| − | = | + | <math> ADCSum^{one channel}=sum_{i=1}^{all pulses}{ADC_{pulse}^{one channel};</math> |
| − | = | + | |
| − | = | + | For distribution over all beam pulses: |
| + | <math> ADC_{ave}=\frac{\sum_{i=1}^{pulses}{ADC_{avg}^{pulse}}}{pulses};</math><br> | ||
| + | <math> ADC_{sigma}={ \sqrt{\frac{1}{pulses}\sum_{i=1}^{pulses}{\left(ADC_{avg}^{pulse} - ADC_{avg}\right)^{2}}}};</math> | ||
| + | |||
Revision as of 03:32, 5 April 2010
FC analysis using ADC channel current distribution
For each ADC channel:
For distribution over all beam pulses:
FC analysis using pulse by pulse ADC channel mean value distribution
For each beam pulse:
For distribution over all beam pulses:
Here is:
1. ADC# = bridge#
2. Pulse# = ReadOut# = Entry# = Event#
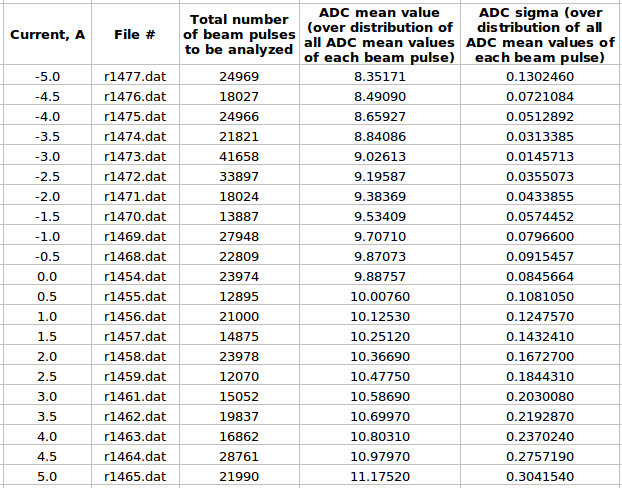
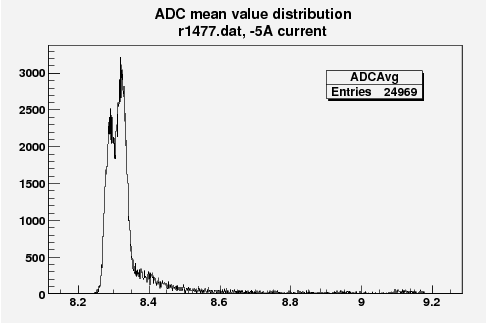
Some examples of ADC mean value distribution. Here are:
1. x axis: ADC mean value for one pulse
2. y axis: number of pulse w/ that ADC mean value
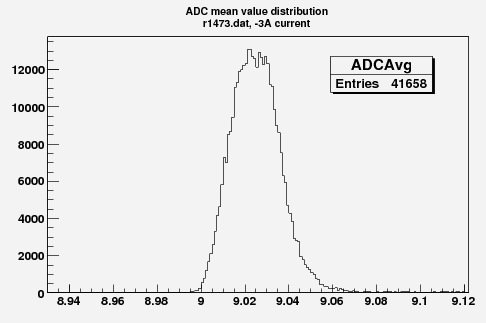
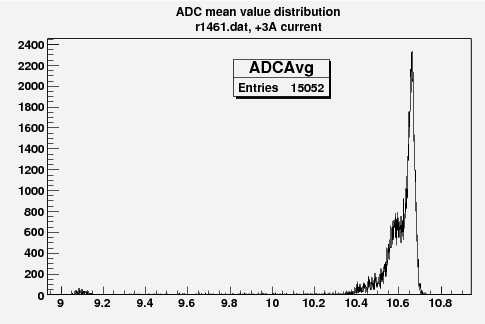
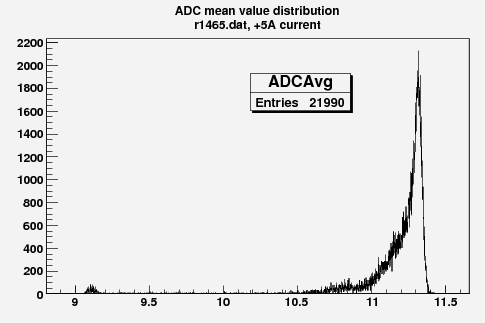
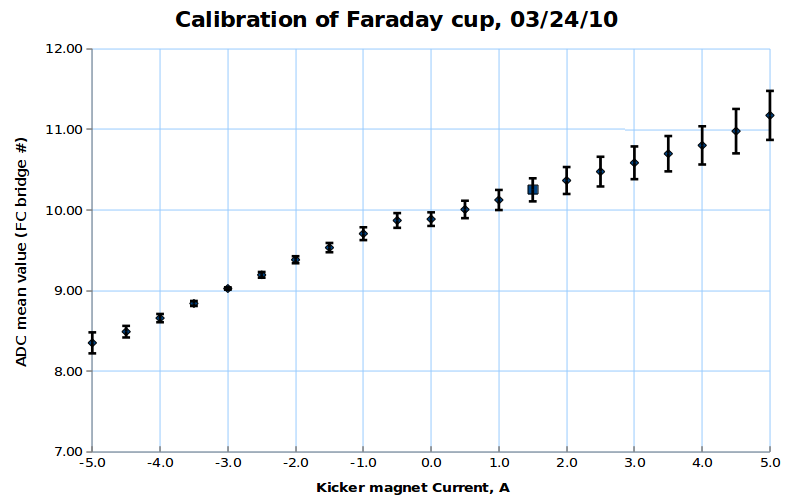
Below is the plot of the charge in Faraday cup (pC) as a function of magnet current (vertical axis, A) (basically magnetic field) and ADC (horizontal axis).