Difference between revisions of "Conversion TDC to Energy"
| Line 17: | Line 17: | ||
where should be in the unit of nano second. | where should be in the unit of nano second. | ||
| + | [[Image:Example.jpg|250px]] | ||
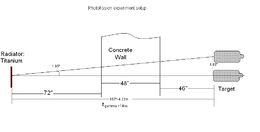
[[ Image:Setup.jpg|260px ]] | [[ Image:Setup.jpg|260px ]] | ||
Revision as of 23:48, 31 October 2008
Method 1:
Calculation
When electron beam hit the radiator, TDC start to count. It will take gamma 14 ns to reach the target. Then after some time , neutron arrive to the detectors.
Let's call the the total time from electron beam hit the radiator to neutron to be detected is . So,
where d is the distance between detector and target, v is speed of neutron. So,
where should be in the unit of nano second.
)
=>
Method 2: Using time difference in two peaks
Calculation
If we assume gamma flash is coming from target, then by time difference in gamma peak and neutron peak, we can tell the energies in neutrons.
: Neutron time of flight
: Gamma time of flight
d: Distance between detector and target.
d for polarized case: = 91.25 inches = 231.775 cm.
d for unpolarized top detector: =96.25 inches = 244.745 cm.
d for unpolarized side detector: =91.39 inches = 232.131 cm.
)
=>
Data
For data go to Link below: