Difference between revisions of "Compton Scattering"
Jump to navigation
Jump to search
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | [http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | ||
| + | |||
| + | |||
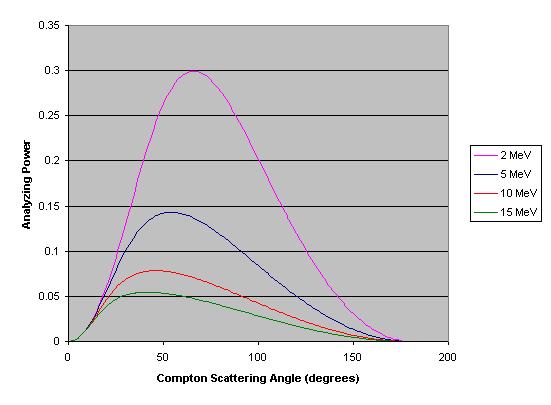
==Analyzing Power as a Function of Compton Scattering Angle== | ==Analyzing Power as a Function of Compton Scattering Angle== | ||
| + | |||
| + | The analyzing power <math></math> | ||
[[Image:power.jpg |800px]] | [[Image:power.jpg |800px]] | ||
| Line 6: | Line 11: | ||
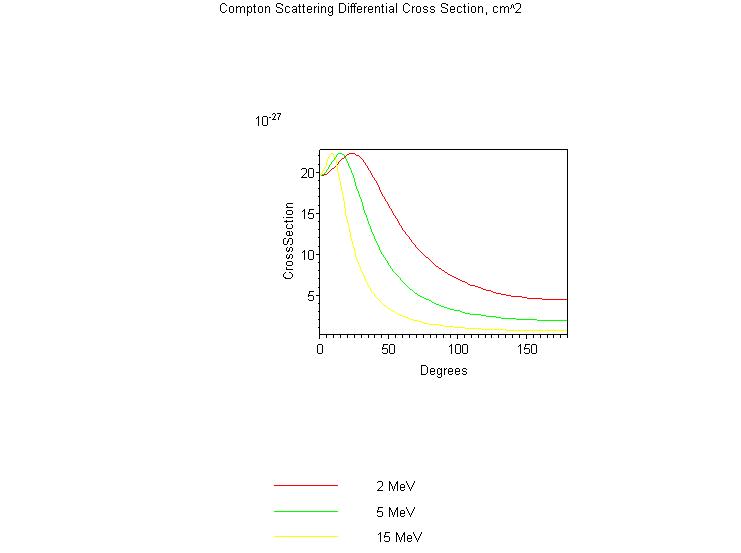
The differential cross section for Compton scattering is given by the Klein-Nishina formula: | The differential cross section for Compton scattering is given by the Klein-Nishina formula: | ||
| − | <math> | + | |
| + | <math>\frac{d\sigma}{d\Omega} = \frac{1}{2} r_e^2 (P(E_\gamma,\theta) - P(E_\gamma,\theta)^2 \sin^2(\theta) + P(E_\gamma,\theta)^3)</math> | ||
[[Image:cross section.jpg |800px]] | [[Image:cross section.jpg |800px]] | ||
| Line 12: | Line 18: | ||
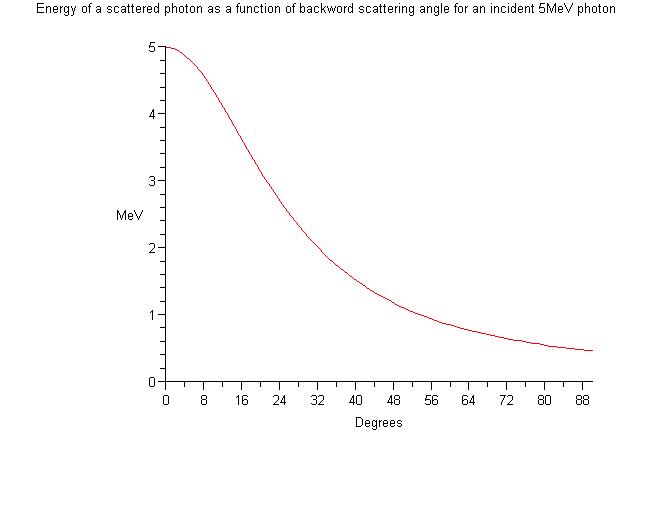
==Energy of Scattered Photon== | ==Energy of Scattered Photon== | ||
[[Image:compton.jpg |800px]] | [[Image:compton.jpg |800px]] | ||
| + | |||
| + | [http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | ||