Difference between revisions of "Compton Scattering"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
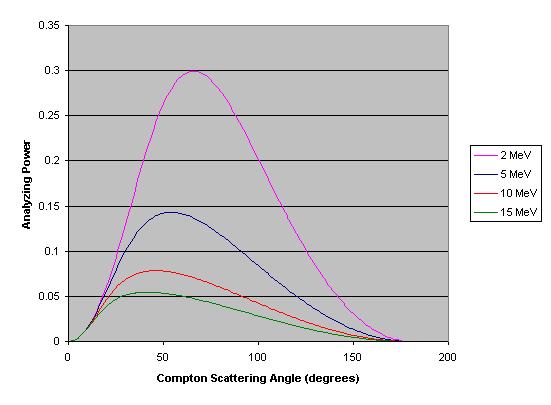
==Analyzing Power as a Function of Compton Scattering Angle== | ==Analyzing Power as a Function of Compton Scattering Angle== | ||
| + | |||
| + | The analyzing power <math>\frac{d\sigma}{d\Omega} = \frac{1}{2} r_e^2 (P(E_\gamma,\theta) - P(E_\gamma,\theta)^2 \sin^2(\theta) + P(E_\gamma,\theta)^3)</math> | ||
[[Image:power.jpg |800px]] | [[Image:power.jpg |800px]] | ||