Difference between revisions of "Forest He-3 Tubes"
| (5 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
<math>n + He^3 \rightarrow p + H^3</math> | <math>n + He^3 \rightarrow p + H^3</math> | ||
| − | About 764 keV of energy is liberated in this nuclear reaction and distributed between the final products according to their masses. Because the proton is about a factor of 3 lighter than Tritium (H^3) , it will have more kinetic energy by about a factor of 3 (about 573 keV). This liberated proton can ionize other He-3 atoms via the reaction | + | About 764 keV of energy is liberated in this nuclear reaction and distributed between the final products according to their masses. |
| + | |||
| + | ;Cons Momentum <math>\Rightarrow</math> | ||
| + | : <math>m_p v_p = m_{H^3} v_{H^3} \Rightarrow v_p = 3v_{H^3}</math> | ||
| + | |||
| + | Because the proton is about a factor of 3 lighter than Tritium (H^3) , it will have more kinetic energy by about a factor of 3 (about 573 keV). This liberated proton can ionize other He-3 atoms via the reaction | ||
<math>p+He^3 \rightarrow p + He^3(+) + e^-</math> | <math>p+He^3 \rightarrow p + He^3(+) + e^-</math> | ||
| Line 24: | Line 29: | ||
: <math>\# protons = \sigma \frac{\# incident particles}{Area}</math> | : <math>\# protons = \sigma \frac{\# incident particles}{Area}</math> | ||
: <math>= \sigma \rho \times L</math> | : <math>= \sigma \rho \times L</math> | ||
| − | + | : <math>= ( 3 \times 10^{-24} cm^2) (10 Atm) \left ( 2.7 \times 10^{19} \frac{atoms}{cm^3} \right ) (76 cm) = 0.06 partices \Rightarrow \epsilon = 6</math> % | |
where | where | ||
| Line 35: | Line 40: | ||
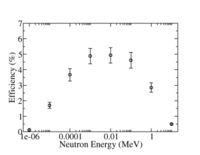
[[Image:He-3Tube_PPND_Efficiency.jpg | 200 px]] | [[Image:He-3Tube_PPND_Efficiency.jpg | 200 px]] | ||
| − | |||
| − | |||
| − | |||
[http://www.iac.isu.edu/mediawiki/index.php/Forest_Detectors Go Back] | [http://www.iac.isu.edu/mediawiki/index.php/Forest_Detectors Go Back] | ||
Latest revision as of 23:33, 22 June 2009
Thermal neutron capture of He-3 may be represented by the reaction below
About 764 keV of energy is liberated in this nuclear reaction and distributed between the final products according to their masses.
- Cons Momentum
Because the proton is about a factor of 3 lighter than Tritium (H^3) , it will have more kinetic energy by about a factor of 3 (about 573 keV). This liberated proton can ionize other He-3 atoms via the reaction
The same proton will ionize several He-3 atoms when dissipating the 573 keV kinetic energy. Once you have the creation of ions, you can construct detectors to collect and measure the electrons.
The Tritium (H^3) can also ionize the gas but due to its higher mass it does not travel as far (shorter range) as the proton and makes a smaller contribution to the ionization signal. Tritium decays to He-3 after about 12 years ( neutron is converted to proton)
reference: J. W. Leake, "Nuclear Instruments and Methods", Vol. 63, page 329, 1968).
The probability of neutron capture is measured in terms of a cross section. There is a nuclear data base for neutron capture located at LBL. The "free" neutron thermal total cross section () is barns ( 1 barn = ).
- Total cross section is defined as
- %
where
- = density of the He-3 target
- L = length of the target.
10-atm He-3, 2.54 cm diameter tube, 76 cm long, poly moderator, cadmium metal, Boron loaded shielding.