Difference between revisions of "HRRL Simulations"
(→Run 1) |
(→Run 1) |
||
| Line 47: | Line 47: | ||
:<math>4.4 \times 10^4 MeV \times \frac{1.6 \times 10^{-19} J }{10^{-6} MeV} = 4.4 \times 10^{-9} J</math> | :<math>4.4 \times 10^4 MeV \times \frac{1.6 \times 10^{-19} J }{10^{-6} MeV} = 4.4 \times 10^{-9} J</math> | ||
| + | In terms of the energy per beam current charge we would have | ||
| + | :\frac{4.4 \times 10^{-9} J}{10^6 e^-} \times \frac{1 e^-}{1.6 \times 10^{-19} C} \times \frac{ | ||
[http://www.iac.isu.edu/mediawiki/index.php/HRRL Go back] | [http://www.iac.isu.edu/mediawiki/index.php/HRRL Go back] | ||
Revision as of 13:12, 11 July 2008
This document describes the simulations performed to estimate the radiological background in the event that a 1 nA electron current from the HRRL enters the experimental cell.
Radiation monitors: Ludlum Model 45-8.
Low energy gamma cutoff = 60 keV
Tungsten SImulation
I created a world volume filled with Air to represent the experimental cell.
I created a 2mm thick tungsten target that is 30 cm x 30 cm in area.
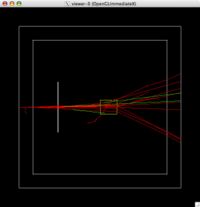
The image below shows several electrons hitting the tungsten foil, then scattering in air. The red lines are electrons and the green ones are photons.
Run 1
I then ran 1 million events in which an incident 7 MeV electron hit the 2 mm thick Tungsten with the physics processes
if (particleName == "gamma") {
// gamma
pmanager->AddDiscreteProcess(new G4PhotoElectricEffect);
pmanager->AddDiscreteProcess(new G4ComptonScattering);
pmanager->AddDiscreteProcess(new G4GammaConversion);
} else if (particleName == "e-") {
//electron
pmanager->AddProcess(new G4MultipleScattering,-1, 1,1);
pmanager->AddProcess(new G4eIonisation, -1, 2,2);
pmanager->AddProcess(new G4eBremsstrahlung, -1, 3,3);
I only kept event in which had a momentum component towards the ceiling
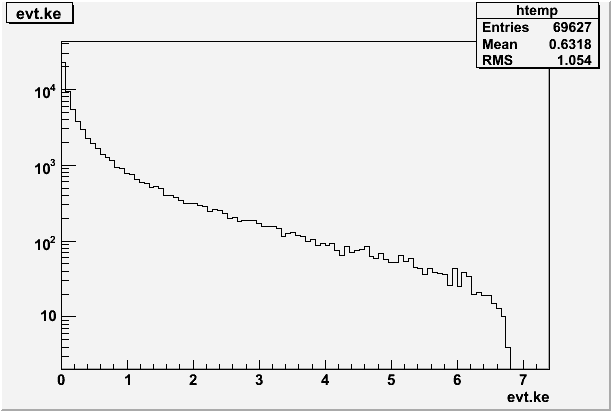
The energy distribution (in MeV) of the gammas headed towards the roof is shown below. Of the 1 million electrons incident on the 2 mm thick Tungsten target, only 70,000 gammas were headed towards the cieling. This does not mean that they hit it, they could have hit the wall.
If I sum the above distribution I see a total energy of 43,987 MeV going up from the 1 million 7 MeV electrons hitting the 2mm Tungsten target.
1 Rad = = the amount of energy absorbed per 100 kg of material
To calculate the worst possible case lets assume all of the radiation is absorbed by a person (there is no concrete ceiling).
Converting the energy from MeV to Joules
In terms of the energy per beam current charge we would have
- \frac{4.4 \times 10^{-9} J}{10^6 e^-} \times \frac{1 e^-}{1.6 \times 10^{-19} C} \times \frac{