Difference between revisions of "Thresholding of Paddles"
| Line 1: | Line 1: | ||
| + | |||
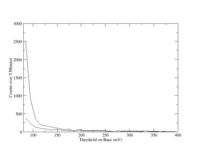
| + | Each paddle has is 4cm by 2cm. The conclusion from these studies shows that the most efficient threshold for the paddles would be at 225mV. We had to map out the tendencies for these paddles because we were unsure of how they worked, that is, we didn't know where the best opperating ranges were. This information is vital if we are to argue that the data we are gathering is actually what we are looking for. | ||
| + | |||
| + | |||
[[Image:DiscriminatorTHreshold.jpg | 200 px]] | [[Image:DiscriminatorTHreshold.jpg | 200 px]] | ||
[[Image:GraphExplanation.jpg | 200 px]] | [[Image:GraphExplanation.jpg | 200 px]] | ||
| − | |||
| − | |||
| − | |||
Latest revision as of 21:14, 10 October 2007
Each paddle has is 4cm by 2cm. The conclusion from these studies shows that the most efficient threshold for the paddles would be at 225mV. We had to map out the tendencies for these paddles because we were unsure of how they worked, that is, we didn't know where the best opperating ranges were. This information is vital if we are to argue that the data we are gathering is actually what we are looking for.
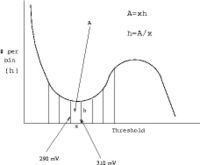
Points of data were taken in 5 minute intervals increasing the threshold by ten mV each time. This means that x is equal to ten mV in these trials. The data received in each interval is equal to the figure A (Area). This is the area of the interval under the curve over the distance x. To find the hight (h), the area A is divided by the distance x.
| Threshold for Base 1 | |||
|---|---|---|---|
| Threshold (mV) | Counts/5 min. | Average | A |
| 80 | 53126 | 53126 | |
| 24959 | |||
| 90 | 28167 | 28167 | |
| 9093 | |||
| 100 | 19074 | 19074 | |
| 3681 | |||
| 110 | 15427, 15358 | 15393 | |
| 1980 | |||
| 120 | 13375, 13450 | 13413 | |
| 160 | 8493 | 8493 | |
| 630 | |||
| 170 | 7863 | 7863 | |
| 794 | |||
| 180 | 7069 | 7069 | |
| 152 | |||
| 190 | 6917 | 6917 | |
| 729 | |||
| 200 | 6188 | 6188 | |
| 357 | |||
| 210 | 5831 | 5831 | |
| 230 | 5315 | 5315 | |
| 462 | |||
| 240 | 4853 | 4853 | |
| 463 | |||
| 250 | 4390 | 4390 | |
| 308 | |||
| 260 | 4236, 4047,
3963 |
4082 | |
| 142 | |||
| 270 | 4254, 3811,
3940, 3754 |
3940 | |
| 250 | |||
| 280 | 3840, 3539 | 3690 | |
| 232 | |||
| 290 | 3458 | 3458 | |
| 191 | |||
| 300 | 3267 | 3267 | |
| 189 | |||
| 310 | 3078 | 3078 | |
| 193 | |||
| 320 | 2871, 2888,
2895 |
2885 | |
| 131 | |||
| 330 | 2767, 2740 | 2754 | |
| 319 | |||
| 340 | 2432, 2423
2440, 2443 |
2435 | |
| 83 | |||
| 350 | 2405, 2412,
2303, 2287 |
2352 | |
| 154 | |||
| 360 | 2217, 2194,
2150, 2232 |
2198 | |
| 150 | |||
| 370 | 2035, 2060 | 2048 | |
| 138 | |||
| 380 | 1910 | 1910 | |
| 127 | |||
| 390 | 1783 | 1783 | |
| 48 | |||
| 400 | 1735 | 1735 | |
| Threshold for Base 2 | |||
|---|---|---|---|
| Threshold (mV) | Counts/5 min. | Average | A |
| 80 | 16574, 16457 | 16516 | |
| 3771 | |||
| 90 | 13131, 12358 | 12745 | |
| 2272 | |||
| 100 | 10509, 10438 | 10473 | |
| 1231 | |||
| 110 | 9223, 9260 | 9242 | |
| 1015 | |||
| 120 | 8133, 8320 | 8227 | |
| 845 | |||
| 130 | 7346, 7418 | 7382 | |
| 562 | |||
| 140 | 6740, 6900 | 6820 | |
| 645 | |||
| 150 | 6176, 6173 | 6175 | |
| 553 | |||
| 160 | 5696, 5548 | 5622 | |
| 351 | |||
| 170 | 5355, 5187 | 5271 | |
| 445 | |||
| 180 | 4782, 4869 | 4826 | |
| 350 | |||
| 190 | 4449, 4502 | 4476 | |
| 363 | |||
| 200 | 4105, 4121 | 4113 | |
| 323 | |||
| 210 | 3893, 3687 | 3790 | |
| 281 | |||
| 220 | 3471, 3547 | 3509 | |
| 190 | |||
| 230 | 3317, 3320 | 3319 | |
| 231 | |||
| 240 | 3094, 3081 | 3088 | |
| 236 | |||
| 250 | 2829, 2874 | 2852 | |
| 176 | |||
| 260 | 2670, 2682 | 2676 | |
| 163 | |||
| 270 | 2557, 2469 | 2513 | |
| 228 | |||
| 280 | 2284, 2286 | 2285 | |
| 181 | |||
| 290 | 2119, 2089 | 2104 | |
| 161 | |||
| 300 | 1956, 1930 | 1943 | |
| 190 | |||
| 310 | 1777, 1729 | 1753 | |
| 120 | |||
| 320 | 1617, 1648 | 1633 | |
| 101 | |||
| 330 | 1544, 1519 | 1532 | |
| 25 | |||
| 340 | 1518, 1472, 1532 | 1507 | |
| 137 | |||
| 350 | 1380, 1360 | 1370 | |
| 117 | |||
| 360 | 1244, 1262 | 1253 | |
| 150 | |||
| 370 | 1102, 1103 | 1103 | |
| 45 | |||
| 380 | 1088, 1028 | 1058 | |
| 28 | |||
| 390 | 1045, 1015 | 1030 | |
| 157 | |||
| 400 | 882, 864 | 873 | |