Difference between revisions of "Forest UCM Osc 2-DOsc"
| (2 intermediate revisions by the same user not shown) | |||
| Line 42: | Line 42: | ||
similarly | similarly | ||
| − | :<math>y = A_y \cos(\omega t^{\prime} - \omega t_0 - \ | + | :<math>y = A_y \cos(\omega t^{\prime} - \omega t_0 - \delta_y)</math> |
| − | ::<math> =A_y \cos(\omega t^{\prime} - \omega \frac{-\delta_x}{\omega} - \ | + | ::<math> =A_y \cos(\omega t^{\prime} - \omega \frac{-\delta_x}{\omega} - \delta_y)</math> |
::<math>= A_y \cos(\omega t^{\prime} +\delta_x - \delta_y)</math> | ::<math>= A_y \cos(\omega t^{\prime} +\delta_x - \delta_y)</math> | ||
::<math>= A_y \cos(\omega t^{\prime} -\delta)</math> | ::<math>= A_y \cos(\omega t^{\prime} -\delta)</math> | ||
| Line 113: | Line 113: | ||
;problem 5.17 a.) show motion is periodic if the ratio of frequencies is a rational number ( p/q) | ;problem 5.17 a.) show motion is periodic if the ratio of frequencies is a rational number ( p/q) | ||
| + | |||
| + | Assume that the ratio of oscillation frequencies is | ||
:<math>\frac{\omega_x}{\omega_y} =\frac{p}{q} </math> where p & q are integers | :<math>\frac{\omega_x}{\omega_y} =\frac{p}{q} </math> where p & q are integers | ||
| Line 118: | Line 120: | ||
The period of the oscillation will be given by | The period of the oscillation will be given by | ||
| − | :<math>\tau = \frac{2 \pi | + | :<math>\tau = \left ( \frac{2 \pi }{\omega_x} \right ) p = \left ( \frac{2 \pi }{\omega_y}\right ) q</math> Definition of period |
: <math>x(t) = A_x \cos(\omega_x t - \delta_x)= A_x \cos(\omega_x t^{\prime})</math> | : <math>x(t) = A_x \cos(\omega_x t - \delta_x)= A_x \cos(\omega_x t^{\prime})</math> | ||
| Line 133: | Line 135: | ||
: <math>y(t+\tau) = A_y \cos(\omega_y (t+\tau) ) - \delta_y)= A_y \cos(\omega_y t+ 2\pi q- \delta) \Rightarrow</math> Motion is periodic | : <math>y(t+\tau) = A_y \cos(\omega_y (t+\tau) ) - \delta_y)= A_y \cos(\omega_y t+ 2\pi q- \delta) \Rightarrow</math> Motion is periodic | ||
| − | ;problem 5.17 | + | ;problem 5.17 b.) show motion is not periodic (no repetition) if the ratio of frequencies is a IR-rational number |
| − | |||
| + | For this solution you just assume the motion is periodic and start the solution to part 5.17 a.) from the end and work backwards. | ||
[[Forest_UCM_Osc#2-D_Oscillators]] | [[Forest_UCM_Osc#2-D_Oscillators]] | ||
Latest revision as of 23:10, 14 October 2021
Two Dimensional Oscillators
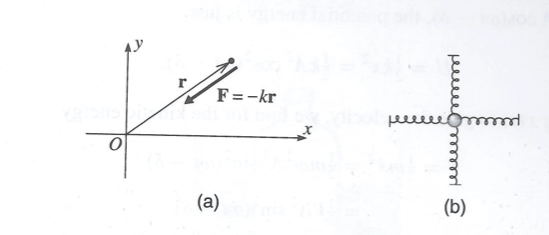
- Potential
Isotropic Oscillator
The simplest 2-D oscillator that is composed of identical springs (same spring constant).
The equations of motion are separable two equations, one for each direction
you could define a relative phase between the two oscillators as
it can be substituted into the above equations by shifting the time origin (problem 5.15)
let
then
let
similarly
Interpretation
There are several modes of motion for the above system of equation
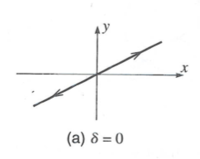
No phase difference
If there is no phase difference then (\delta =0 ) and you have oscillating motion along a line.
90 degree phase difference
If the x and y motions are completely out of phase ( phase difference of 90 degrees or )
then the motion is an ellipse (unless their amplitudes are equal in which case the mass moves in a circle).
The above is an equation of a circle if otherwise it is an ellipse with semi-major and semi-minor axes and
If the phase shift is less than 90 then the ellipse is slanted towards the x-axis otherwise it is toward the y-axis.
Anisotropic Oscillator
Consider the case of having two different spring constants in each direction
The equations of motion are separable two equations, one for each direction
where
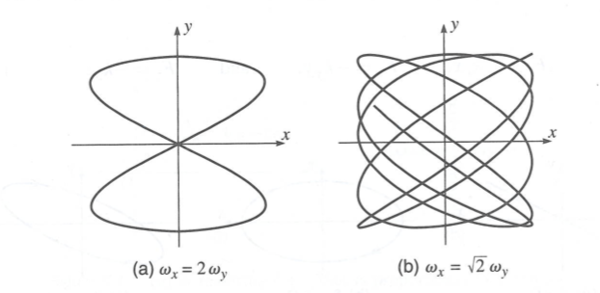
Lissajous figure
if
- rational number (a fraction formed two integers, denominator is non-zero)
then the motion repeats itself.
If the ratio is irrational the motion does not repreat.
- problem 5.17 a.) show motion is periodic if the ratio of frequencies is a rational number ( p/q)
Assume that the ratio of oscillation frequencies is
- where p & q are integers
The period of the oscillation will be given by
- Definition of period
The solution for the next period is
- Motion is periodic
- if p is an integer
Similarly for the y-direction
- Motion is periodic
- problem 5.17 b.) show motion is not periodic (no repetition) if the ratio of frequencies is a IR-rational number
For this solution you just assume the motion is periodic and start the solution to part 5.17 a.) from the end and work backwards.