Difference between revisions of "LB Thesis NewSNR Corrections"
| Line 10: | Line 10: | ||
"Since, as already mentioned, yield values are normalized for a common exposure period of one hour, the following expression is required, which converts the individual activities yielded using other irradiation times to those after standard exposure period T (1h): | "Since, as already mentioned, yield values are normalized for a common exposure period of one hour, the following expression is required, which converts the individual activities yielded using other irradiation times to those after standard exposure period T (1h): | ||
| − | <math> N(T) = \frac{A_{0,el}}{A_{0,Ni}} \times \frac{(1-e^{-\lambda_{el}T})}{(1-e^{- \ | + | <math> N(T) = \frac{A_{0,el}}{A_{0,Ni}} \times \frac{(1-e^{-\lambda_{el}T})}{(1-e^{- \lambda_{el} T_i})} \times \frac{(1-e^{- \lambda_{Ni} T_i})}{(1-e^{-\lambda_{Ni} T})} </math> |
| + | |||
| + | Where <math> T_i </math> is the actual exposure period and T is the normalized exposure period of 1 hour" | ||
| + | |||
| + | So lets try to correct these ratios using Nickel | ||
| + | |||
| + | For correcting the 50%, we have (note these are the fixed fit values) | ||
| + | |||
| + | <math> N(T) = 0.62 \times \frac{0.52}{0.32} \times \frac{0.01}{0.02} = 0.50 </math> | ||
| + | |||
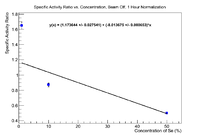
| + | This ratio is lower than its original value (0.62), which makes sense because the nickel would not die off as much in the beam. The 10% and 1% values should not need this correction as they were irradiated for an hour, so the correction goes to unity. Plot the ratio of the specific activity as a function of concentration. | ||
| + | |||
| + | [[File:Se81m SpecificActivityRatiovsConcentration SegebadeNormalized.png|200px]] | ||
Revision as of 16:07, 25 July 2018
First plot the efficiency corrected activity as a function of concentration. These points are not weighted by mass, but they are fully corrected as per the thesis otherwise. These values are the activity at the highest value of N/B
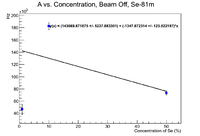
This plot doesn't look very good as the 50% sample has a lower activity than the 10% sample. Try plotting this at the time of beam off. Note these are done using fits with the accepted half life vs. the experimental half life. The error bars represent |(Free Fit A) - (Fixed Fit A)|
Perhaps the difference comes from the fact that the irradiation times were different, but to normalize to a standard beam time, a reference material must be used. Segebade says "Since, as already mentioned, yield values are normalized for a common exposure period of one hour, the following expression is required, which converts the individual activities yielded using other irradiation times to those after standard exposure period T (1h):
Where is the actual exposure period and T is the normalized exposure period of 1 hour"
So lets try to correct these ratios using Nickel
For correcting the 50%, we have (note these are the fixed fit values)
This ratio is lower than its original value (0.62), which makes sense because the nickel would not die off as much in the beam. The 10% and 1% values should not need this correction as they were irradiated for an hour, so the correction goes to unity. Plot the ratio of the specific activity as a function of concentration.