Difference between revisions of "Linac Run Plan April 2018, Dr. McNulty"

From New IAC Wiki
Jump to navigation Jump to search
Line 209: Line 209:
  
 
Average dose per pulse <math>\frac{0.0147657\ J}{14.9296*10^{-3}\ Kg}=0.98902\ Gy=98.902\ rad</math>
 
Average dose per pulse <math>\frac{0.0147657\ J}{14.9296*10^{-3}\ Kg}=0.98902\ Gy=98.902\ rad</math>
 +
 +
==5mA, 100ns pulse width, 100cm from beam pipe==
 +
 +
Changed distance from end of beam pipe from 25cm to 50cm.
 +
 +
Cut current by a factor of 4. 100mA->25mA
 +
 +
Assuming <math>25\frac{mA}{pulse}</math> and a pulse width of <math>100ns</math>
 +
 +
Then <math>25\frac{mA}{pulse}=25\frac{mC}{s*pulse}=0.025\frac{C}{s*pulse}</math>
 +
 +
<math>0.025\frac{C}{s*pulse}(100ns)=2.5*10^{-9}\frac{C}{pulse}</math>
 +
 +
<math>2.5*10^{-9}\frac{C}{pulse}*\frac{1\ e-}{1.602*10^{-19}}=1.56055*10^{10}\frac{e-}{pulse}</math>
 +
 +
===OSL===
 +
 +
<math>\frac{1}{1000}</math> of a pulse. ~15mil e- simulated, ~15bil e- per pulse. With beam parameters given above.
 +
 +
Deposited Energy: <math>9.29701*10^{5} MeV</math>
 +
 +
OSL geometry: 0.501cm diameter cylinder of 0.03cm thickness with beam incident on flat face.
 +
 +
OSL Crystal density<math>=3.9698\frac{g}{cm^{3}}</math>
 +
 +
Mass of a single OSL crystal: <math>(\pi(0.2505)^{2}*(0.03))*(3.9698)=0.0234777g</math>
 +
 +
Scaling deposited energy by 1000 to account for only shooting a 1000th of a pulse, the deposited energy becomes <math>9.29701*10^{8} MeV</math>
 +
 +
Converting to Joules for dose calculation: <math>9.29701*10^{8} MeV=1.48938*10^{-4}J</math>
 +
 +
Average dose per pulse: <math>\frac{1.48938*10^{-4}J}{0.0234777*10^{-3}\ Kg}=6.34381\ Gy=634.381\ rad</math>
 +
 +
===Quartz===
 +
 +
<math>\frac{1}{1000}</math> of a pulse. ~15mil e- simulated, ~15bil e- per pulse. With beam parameters given above.
 +
 +
Deposited Energy: <math>9.21601*10^{7} MeV</math>
 +
 +
Quartz Geometry: 1 inch diameter, 0.5 inch tall cylinder with electrons incident upon the base of the cylinder.
 +
 +
Quartz density<math>=2.32\frac{g}{cm^{3}}</math>
 +
 +
Mass of Quartz used in simulation: <math>(\pi(1.27)^{2}*(1.27))*(2.32)=14.9296g</math>
 +
 +
Scaling deposited energy by 1000 to account for only shooting a 1000th of a pulse, the deposited energy becomes <math>9.21601*10^{10} MeV</math>
 +
 +
Converting to Joules for dose calculation: <math>9.21601*10^{10} MeV=0.0147657J</math>
 +
 +
Average dose per pulse <math>\frac{0.0147657\ J}{14.9296*10^{-3}\ Kg}=0.98902\ Gy=98.902\ rad</math>
 +
 +
===Plastic (Polyethylene)===
  
 
==25mA, 100ns pulse width, 50cm from beam pipe, tungsten target with aluminum beamstop==
 
==25mA, 100ns pulse width, 50cm from beam pipe, tungsten target with aluminum beamstop==

Revision as of 18:55, 26 May 2018

Beam Line info

0 degree line

Aluminum window = 0.5mm thick. Radius = 23.813mm

Air gap between Aluminum window and glass slide = 45mm

Glass slide Thickness = 1mm

Run Plan

To find operating point

- Will use 15 OSLs from reproducibility study to make sure that dose is within acceptable range

Experiment

85 Nanodot OSLs for use (dose not include OSLs from reproducibility study)

- upper limit of OSLs is 15Gy, want to be around 7.5Gy with multiple pulses

Machine: 25b Linac

Beam Energy: 8 MeV

Rep Rate: Max (150Hz)

Will talk to engineers about double pulsing and guaranteeing number of pulses and update.

Shot # Start Time End Time Number of Pulses Number of OSLs Distance to end of beampipe Beam Current Aluminum Brick
1 7:00am 7:05am 2 1 1m 5 mA Out
2 7:10am 7:15am 2 1 1m 10 mA Out
3 7:20am 7:25am 2 1 1m 25 mA Out
4 7:30am 7:35am 2 1 1m 50 mA Out
5 7:40am 7:45am 2 1 1m 25 mA Out
6 7:50am 7:55am 2 1 1m 25 mA Out
7 8:00am 8:05am 2 16 1m 25 mA In
8 8:10am 8:15am 2 16 1m 25 mA In
9 8:20am 8:25am 2 16 1m 25 mA Out
10 8:30am 8:35am 2 16 1m 25 mA Out
11 8:40am 8:45am 2 16 1m 25 mA Out


Highest single pulse simulated parameters are 25mA with 100ns pulse width.

Absorbed Dose Information

100mA, 100ns pulse width, 25cm from beam pipe

Assuming [math]100\frac{mA}{pulse}[/math] and a pulse width of [math]100ns[/math]

Then [math]100\frac{mA}{pulse}=100\frac{mC}{s*pulse}=0.1\frac{C}{s*pulse}[/math]

[math]0.1\frac{C}{s*pulse}(100ns)=10*10^{-9}\frac{C}{pulse}[/math]

[math]10*10^{-9}\frac{C}{pulse}*\frac{1\ e-}{1.602*10^{-19}}=6.2422*10^{10}\frac{e-}{pulse}[/math]

Using a distance of 25cm for all simulations following.

OSL

[math]\frac{1}{1000}[/math] of a pulse. ~62mil e- simulated, ~62bil e- per pulse. With beam parameters given above.

Deposited Energy: [math]4.46596*10^{6} MeV[/math]

OSL geometry: 0.501cm diameter cylinder of 0.03cm thickness with beam incident on flat face.

OSL Crystal density[math]=3.9698\frac{g}{cm^{3}}[/math]

Mass of a single OSL crystal: [math](\pi(0.2505)^{2}*(0.03))*(3.9698)=0.0234777g[/math]

Scaling deposited energy by 1000 to account for only shooting a 1000th of a pulse, the deposited energy becomes [math]4.46596*10^{9} MeV[/math]

Converting to Joules for dose calculation: [math]4.46596*10^{9} MeV=7.15525*10^{-4}J[/math]

Average dose per pulse [math]\frac{7.15525*10^{-4}J}{0.0234777*10^{-3}\ Kg}=30.4768\ Gy=3047.68\ rad[/math]

Quartz

[math]\frac{1}{1000}[/math] of a pulse. ~62mil e- simulated, ~62bil e- per pulse. With beam parameters given above.

Deposited Energy: [math]4.71875*10^{8} MeV[/math]

Quartz Geometry: 1 inch cylinder with electrons incident upon the base of the cylinder.

Quartz density[math]=2.32\frac{g}{cm^{3}}[/math]

Mass of Quartz used in simulation: [math](\pi(1.27)^{2}*(2.54))*(2.32)=29.8593g[/math]

Scaling deposited energy by 1000 to account for only shooting a 1000th of a pulse, the deposited energy becomes [math]4.71875*10^{11} MeV[/math]

Converting to Joules for dose calculation: [math]4.71875*10^{11} MeV=0.0756027J[/math]

Average dose per pulse [math]\frac{0.0756027\ J}{29.8593*10^{-3}\ Kg}=2.53196\ Gy=253.196\ rad[/math]

25mA, 100ns pulse width, 25cm from beam pipe

Cut current by a factor of 4. 100mA->25mA

Assuming [math]25\frac{mA}{pulse}[/math] and a pulse width of [math]100ns[/math]

Then [math]25\frac{mA}{pulse}=25\frac{mC}{s*pulse}=0.025\frac{C}{s*pulse}[/math]

[math]0.025\frac{C}{s*pulse}(100ns)=2.5*10^{-9}\frac{C}{pulse}[/math]

[math]2.5*10^{-9}\frac{C}{pulse}*\frac{1\ e-}{1.602*10^{-19}}=1.56055*10^{10}\frac{e-}{pulse}[/math]

Using a distance of 25cm for all simulations following.

OSL

[math]\frac{1}{1000}[/math] of a pulse. ~15mil e- simulated, ~15bil e- per pulse. With beam parameters given above.

Deposited Energy: [math]1.11636*10^{6} MeV[/math]

OSL geometry: 0.501cm diameter cylinder of 0.03cm thickness with beam incident on flat face.

OSL Crystal density[math]=3.9698\frac{g}{cm^{3}}[/math]

Mass of a single OSL crystal: [math](\pi(0.2505)^{2}*(0.03))*(3.9698)=0.0234777g[/math]

Scaling deposited energy by 1000 to account for only shooting a 1000th of a pulse, the deposited energy becomes [math]1.11636*10^{9} MeV[/math]

Converting to Joules for dose calculation: [math]1.11636*10^{9} MeV=1.78841*10^{-4}J[/math]

Average dose per pulse [math]\frac{1.78841*10^{-4}J}{0.0234777*10^{-3}\ Kg}=7.61748\ Gy=761.748\ rad[/math]

Quartz

[math]\frac{1}{1000}[/math] of a pulse. ~15mil e- simulated, ~15bil e- per pulse. With beam parameters given above.

Deposited Energy: [math]9.82027*10^{7} MeV[/math]

Quartz Geometry: 1 inch diameter, 0.5 inch tall cylinder with electrons incident upon the base of the cylinder.

Quartz density[math]=2.32\frac{g}{cm^{3}}[/math]

Mass of Quartz used in simulation: [math](\pi(1.27)^{2}*(1.27))*(2.32)=14.9296g[/math]

Scaling deposited energy by 1000 to account for only shooting a 1000th of a pulse, the deposited energy becomes [math]9.82027*10^{10} MeV[/math]

Converting to Joules for dose calculation: [math]9.82027*10^{10} MeV=0.0157321J[/math]

Average dose per pulse [math]\frac{0.0157321\ J}{14.9296*10^{-3}\ Kg}=1.05375\ Gy=105.375\ rad[/math]

25mA, 100ns pulse width, 50cm from beam pipe

Changed distance from end of beam pipe from 25cm to 50cm.

Cut current by a factor of 4. 100mA->25mA

Assuming [math]25\frac{mA}{pulse}[/math] and a pulse width of [math]100ns[/math]

Then [math]25\frac{mA}{pulse}=25\frac{mC}{s*pulse}=0.025\frac{C}{s*pulse}[/math]

[math]0.025\frac{C}{s*pulse}(100ns)=2.5*10^{-9}\frac{C}{pulse}[/math]

[math]2.5*10^{-9}\frac{C}{pulse}*\frac{1\ e-}{1.602*10^{-19}}=1.56055*10^{10}\frac{e-}{pulse}[/math]

OSL

[math]\frac{1}{1000}[/math] of a pulse. ~15mil e- simulated, ~15bil e- per pulse. With beam parameters given above.

Deposited Energy: [math]9.29701*10^{5} MeV[/math]

OSL geometry: 0.501cm diameter cylinder of 0.03cm thickness with beam incident on flat face.

OSL Crystal density[math]=3.9698\frac{g}{cm^{3}}[/math]

Mass of a single OSL crystal: [math](\pi(0.2505)^{2}*(0.03))*(3.9698)=0.0234777g[/math]

Scaling deposited energy by 1000 to account for only shooting a 1000th of a pulse, the deposited energy becomes [math]9.29701*10^{8} MeV[/math]

Converting to Joules for dose calculation: [math]9.29701*10^{8} MeV=1.48938*10^{-4}J[/math]

Average dose per pulse: [math]\frac{1.48938*10^{-4}J}{0.0234777*10^{-3}\ Kg}=6.34381\ Gy=634.381\ rad[/math]

Quartz

[math]\frac{1}{1000}[/math] of a pulse. ~15mil e- simulated, ~15bil e- per pulse. With beam parameters given above.

Deposited Energy: [math]9.21601*10^{7} MeV[/math]

Quartz Geometry: 1 inch diameter, 0.5 inch tall cylinder with electrons incident upon the base of the cylinder.

Quartz density[math]=2.32\frac{g}{cm^{3}}[/math]

Mass of Quartz used in simulation: [math](\pi(1.27)^{2}*(1.27))*(2.32)=14.9296g[/math]

Scaling deposited energy by 1000 to account for only shooting a 1000th of a pulse, the deposited energy becomes [math]9.21601*10^{10} MeV[/math]

Converting to Joules for dose calculation: [math]9.21601*10^{10} MeV=0.0147657J[/math]

Average dose per pulse [math]\frac{0.0147657\ J}{14.9296*10^{-3}\ Kg}=0.98902\ Gy=98.902\ rad[/math]

5mA, 100ns pulse width, 100cm from beam pipe

Changed distance from end of beam pipe from 25cm to 50cm.

Cut current by a factor of 4. 100mA->25mA

Assuming [math]25\frac{mA}{pulse}[/math] and a pulse width of [math]100ns[/math]

Then [math]25\frac{mA}{pulse}=25\frac{mC}{s*pulse}=0.025\frac{C}{s*pulse}[/math]

[math]0.025\frac{C}{s*pulse}(100ns)=2.5*10^{-9}\frac{C}{pulse}[/math]

[math]2.5*10^{-9}\frac{C}{pulse}*\frac{1\ e-}{1.602*10^{-19}}=1.56055*10^{10}\frac{e-}{pulse}[/math]

OSL

[math]\frac{1}{1000}[/math] of a pulse. ~15mil e- simulated, ~15bil e- per pulse. With beam parameters given above.

Deposited Energy: [math]9.29701*10^{5} MeV[/math]

OSL geometry: 0.501cm diameter cylinder of 0.03cm thickness with beam incident on flat face.

OSL Crystal density[math]=3.9698\frac{g}{cm^{3}}[/math]

Mass of a single OSL crystal: [math](\pi(0.2505)^{2}*(0.03))*(3.9698)=0.0234777g[/math]

Scaling deposited energy by 1000 to account for only shooting a 1000th of a pulse, the deposited energy becomes [math]9.29701*10^{8} MeV[/math]

Converting to Joules for dose calculation: [math]9.29701*10^{8} MeV=1.48938*10^{-4}J[/math]

Average dose per pulse: [math]\frac{1.48938*10^{-4}J}{0.0234777*10^{-3}\ Kg}=6.34381\ Gy=634.381\ rad[/math]

Quartz

[math]\frac{1}{1000}[/math] of a pulse. ~15mil e- simulated, ~15bil e- per pulse. With beam parameters given above.

Deposited Energy: [math]9.21601*10^{7} MeV[/math]

Quartz Geometry: 1 inch diameter, 0.5 inch tall cylinder with electrons incident upon the base of the cylinder.

Quartz density[math]=2.32\frac{g}{cm^{3}}[/math]

Mass of Quartz used in simulation: [math](\pi(1.27)^{2}*(1.27))*(2.32)=14.9296g[/math]

Scaling deposited energy by 1000 to account for only shooting a 1000th of a pulse, the deposited energy becomes [math]9.21601*10^{10} MeV[/math]

Converting to Joules for dose calculation: [math]9.21601*10^{10} MeV=0.0147657J[/math]

Average dose per pulse [math]\frac{0.0147657\ J}{14.9296*10^{-3}\ Kg}=0.98902\ Gy=98.902\ rad[/math]

Plastic (Polyethylene)

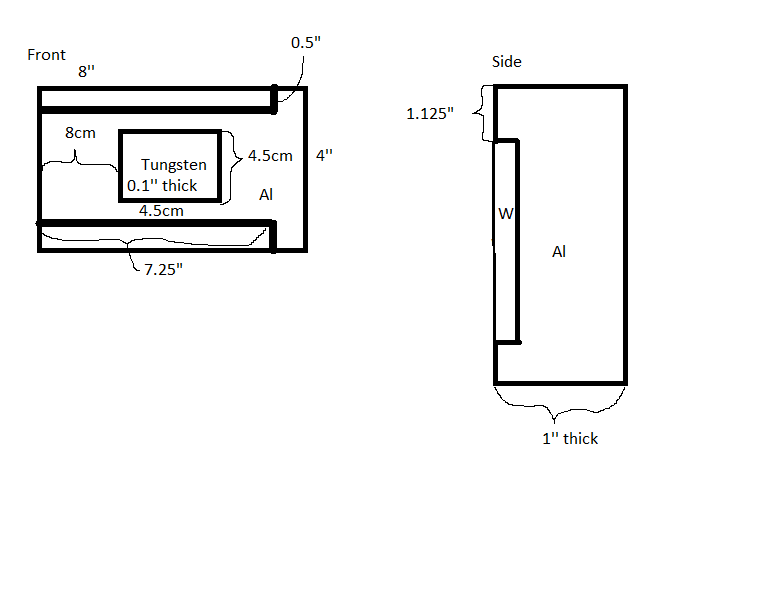
25mA, 100ns pulse width, 50cm from beam pipe, tungsten target with aluminum beamstop

Added .254cm of Tungsten and 2.286cm of Aluminum to be used as converter and beam stop.

Radiator.png

Assuming [math]25\frac{mA}{pulse}[/math] and a pulse width of [math]100ns[/math]

Then [math]25\frac{mA}{pulse}=25\frac{mC}{s*pulse}=0.025\frac{C}{s*pulse}[/math]

[math]0.025\frac{C}{s*pulse}(100ns)=2.5*10^{-9}\frac{C}{pulse}[/math]

[math]2.5*10^{-9}\frac{C}{pulse}*\frac{1\ e-}{1.602*10^{-19}}=1.56055*10^{10}\frac{e-}{pulse}[/math]

OSL (8MeV)

[math]\frac{1}{1000}[/math] of a pulse. ~15mil e- simulated, ~15bil e- per pulse. With beam parameters given above.

Deposited Energy: [math]19.1759 MeV[/math]

OSL geometry: 0.501cm diameter cylinder of 0.03cm thickness with beam incident on flat face.

OSL Crystal density[math]=3.9698\frac{g}{cm^{3}}[/math]

Mass of a single OSL crystal: [math](\pi(0.2505)^{2}*(0.03))*(3.9698)=0.0234777g[/math]

Scaling deposited energy by 1000 to account for only shooting a 1000th of a pulse, the deposited energy becomes [math]9.29701*10^{8} MeV[/math]

Converting to Joules for dose calculation: [math]19.1759*10^{3} MeV=3.0723177*10^{-9}J[/math]

Average dose per pulse: [math]\frac{3.0723177*10^{-9}J}{0.0234777*10^{-3}\ Kg}=0.000130861\ Gy=0.0130861\ rad[/math]


Thesis

Retrieved from "https://wiki.iac.isu.edu/index.php?title=Linac_Run_Plan_April_2018,_Dr._McNulty&oldid=123205"