Difference between revisions of "Relativistic Frames of Reference"
| (13 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <center><math>\ | + | <center><math> \underline{\textbf{Navigation} }</math> |
[[Uniform_distribution_in_Energy_and_Theta_LUND_files|<math>\vartriangleleft </math>]] | [[Uniform_distribution_in_Energy_and_Theta_LUND_files|<math>\vartriangleleft </math>]] | ||
| − | [[VanWasshenova_Thesis# | + | [[VanWasshenova_Thesis#Moller_Scattering|<math>\triangle </math>]] |
| − | [[ | + | [[Relativistic_Units|<math>\vartriangleright </math>]] |
</center> | </center> | ||
| Line 19: | Line 19: | ||
In the rest frame of v=0 | In the rest frame of v=0 | ||
| − | <center><math>\begin{cases} | + | <center><math>v=0 \Rightarrow \begin{cases} |
t= t' \\ | t= t' \\ | ||
| Line 28: | Line 28: | ||
z=z'+vt' | z=z'+vt' | ||
\end{cases}</math></center> | \end{cases}</math></center> | ||
| + | |||
| + | While conversely, from the rest frame of v'=0 | ||
| + | |||
| + | <center><math>v'=0 \Rightarrow \begin{cases} | ||
| + | t'= t \\ | ||
| + | |||
| + | x'=x \\ | ||
| + | |||
| + | y'=y \\ | ||
| + | |||
| + | z'=z-vt | ||
| + | \end{cases}</math></center> | ||
| + | |||
| + | |||
| Line 47: | Line 61: | ||
| − | <center><math>c=\frac{\sqrt{\Delta x^2+\Delta y^2+\Delta z^2}}{t}</math></center> | + | <center><math>c=\frac{\sqrt{\Delta x^2+\Delta y^2+\Delta z^2}}{\Delta t}</math></center> |
| Line 53: | Line 67: | ||
| − | <center><math>c=\frac{\sqrt{\Delta x^{'2}+\Delta y^{'2}+\Delta z^{'2}}}{t}</math></center> | + | <center><math>c=\frac{\sqrt{\Delta x^{'2}+\Delta y^{'2}+\Delta z^{'2}}}{\Delta t}</math></center> |
| Line 80: | Line 94: | ||
| − | <center><math> | + | <center><math>ds^2\equiv c^2 dt^{'2}-dx^{'2}-dy^{'2}-dz^{'2}= c^2 dt^{2}-dx^2-dy^2-dz^2</math></center> |
Since the speed of light is a constant for all frames of reference, this allows the space time interval to also be invariant for inertial frames. | Since the speed of light is a constant for all frames of reference, this allows the space time interval to also be invariant for inertial frames. | ||
| − | <center><math> | + | <center><math>ds^2\equiv c^2 dt^{'2}-dx^{'2}-dy^{'2}-dz^{'2}= c^2 dt^{2}-dx^2-dy^2-dz^2</math></center> |
| − | <center><math> | + | <center><math>ds^2\equiv c^2 dt^{'2}-dr^{'2}= c^2 dt^{2}-dr^2</math></center> |
| − | <center><math> | + | <center><math>ds^2\equiv (c^2 -v^{'2})dt^{'2}= (c^2 -v^2)dt^{2}</math></center> |
| Line 97: | Line 111: | ||
| − | <center><math> | + | <center><math>ds^2\equiv c^2 dt^{'2}= (c^2 -v^2)dt^{2}</math></center> |
| Line 133: | Line 147: | ||
<center><math> | <center><math> | ||
| + | v=0\Rightarrow | ||
\begin{cases} | \begin{cases} | ||
t= t' \\ | t= t' \\ | ||
| Line 154: | Line 169: | ||
</math></center> | </math></center> | ||
| − | <center><math> | + | |
| + | <center><math>v'=0\Rightarrow | ||
\begin{cases} | \begin{cases} | ||
t'= t' \\ | t'= t' \\ | ||
| Line 179: | Line 195: | ||
| − | <center><math>\ | + | <center><math> \underline{\textbf{Navigation} }</math> |
[[Uniform_distribution_in_Energy_and_Theta_LUND_files|<math>\vartriangleleft </math>]] | [[Uniform_distribution_in_Energy_and_Theta_LUND_files|<math>\vartriangleleft </math>]] | ||
| − | [[VanWasshenova_Thesis# | + | [[VanWasshenova_Thesis#Moller_Scattering|<math>\triangle </math>]] |
| − | [[ | + | [[Relativistic_Units|<math>\vartriangleright </math>]] |
</center> | </center> | ||
Latest revision as of 18:45, 15 May 2018
Relativistic Frames of Reference
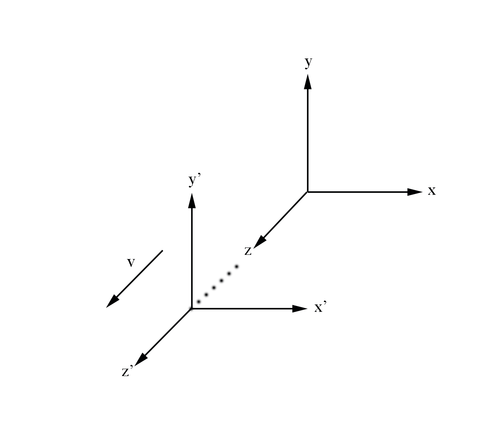
From the Galilean description of motion for a frame of reference moving relative to another frame considered stationary we know that
In the rest frame of v=0
While conversely, from the rest frame of v'=0
Using Einstein's Theory of Relativity, we know that the speed of light is a constant, c, for all reference frames. In the unprimed frame, from the definition of speed:
where
Using the distance equation in a Cartesian coordinate system, the equation for the speed of light becomes
Following the postulate of Special Relativity, this implies for the primed frame
We can rewrite this as
This is possible since the ratios of distance to time are multiples of the same base, i.e. the square of the speed of light . Therefore for the relative change in the time in one frame, the distance must change by the same factor to maintain the same constant. With this we can write
This quantity is known as the time space interval when the change is infinitesimal
Since the speed of light is a constant for all frames of reference, this allows the space time interval to also be invariant for inertial frames.
From the rest frame of v'=0
Assuming motion is only along the z direction
Substituting these changes into the Galilean transformations