Difference between revisions of "TF SPIM e-gamma"
| (10 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
=== Bremsstrahlung=== | === Bremsstrahlung=== | ||
;Definition: Radiation produced when a charged particle is deflected by the electric field of nuclei in a material. | ;Definition: Radiation produced when a charged particle is deflected by the electric field of nuclei in a material. | ||
| Line 17: | Line 16: | ||
:<math>Z</math> = Atomic number = number of protons in target material | :<math>Z</math> = Atomic number = number of protons in target material | ||
: <math>\gamma = \frac{100 m_ec^2 h \nu}{E_0 E Z^{1/3}}</math> = charge screening parameter | : <math>\gamma = \frac{100 m_ec^2 h \nu}{E_0 E Z^{1/3}}</math> = charge screening parameter | ||
| − | Coulomb correction to using the Born approximation (approximation assumes the incident particle is a plane wave interacting with a static E-field the correction accounts for changes | + | Coulomb correction to using the Born approximation (approximation assumes the incident particle is a plane wave interacting with a static E-field, the correction accounts for changes in the plane wave due to the presence of the field). Charge screening and the coulomb correction are different effects that have been shown to be additive/independent. [[File:Haug_2008.pdf]] |
:<math>f(Z) = (Z \alpha)^2 \sum_1^{\infty} \frac{1}{ n [ n^2 + (Z \alpha)^2]}</math> | :<math>f(Z) = (Z \alpha)^2 \sum_1^{\infty} \frac{1}{ n [ n^2 + (Z \alpha)^2]}</math> | ||
: <math>\sim (Z \alpha)^2 \left \{ \frac{1}{1+(Z \alpha)^2} +0.20206 - 0.0369(Z \alpha)^2 + 0.0083 (Z \alpha)^4 - 0.002 (Z \alpha)^6\right \}</math> | : <math>\sim (Z \alpha)^2 \left \{ \frac{1}{1+(Z \alpha)^2} +0.20206 - 0.0369(Z \alpha)^2 + 0.0083 (Z \alpha)^4 - 0.002 (Z \alpha)^6\right \}</math> | ||
| Line 49: | Line 48: | ||
: <math>N = \frac{ number\; atoms}{cm^3} = \frac{\rho N_a}{A} = \frac{density \;\times\; Avagadros\;\;Number}{Atomic number}</math> | : <math>N = \frac{ number\; atoms}{cm^3} = \frac{\rho N_a}{A} = \frac{density \;\times\; Avagadros\;\;Number}{Atomic number}</math> | ||
:<math>\left ( h \nu \right )</math> = Energy of emmitted photon | :<math>\left ( h \nu \right )</math> = Energy of emmitted photon | ||
| − | :<math>\left ( \frac{d \sigma}{d \nu} \right )</math> = | + | :<math>\left ( \frac{d \sigma}{d \nu} \right )</math> = Probability of Energy loss |
| Line 77: | Line 76: | ||
[[Image:SPIM_Bethe-Brem_Eloss-vs-Energy.jpg | 600 px]] | [[Image:SPIM_Bethe-Brem_Eloss-vs-Energy.jpg | 600 px]] | ||
| + | |||
| + | The energy loss, due to collisions, of a proton is overlaid for comparison. | ||
;Critical Energy<math> E_C</math>: | ;Critical Energy<math> E_C</math>: | ||
| Line 205: | Line 206: | ||
;Examples of Radiation length | ;Examples of Radiation length | ||
| − | ;<math>\frac{1}{e} = \frac{1}{2.72} \sim \frac{1}{3}</math> : an electron has | + | ;<math>\frac{1}{e} = \frac{1}{2.72} \sim \frac{1}{3}</math> : an electron has 1/3 of its original energy after traveling 1 radiation length (1 <math>X_0</math>) through the material |
| − | ;<math>\frac{1}{e^2} \sim \frac{1}{7}</math> : an electron has | + | ;<math>\frac{1}{e^2} \sim \frac{1}{7}</math> : an electron has 1/7 of its original energy after traveling 2 radiation lengths (2 <math>X_0</math>) through the material |
| − | ;<math>\frac{1}{e^3} \sim \frac{1}{20}</math> : an electron has | + | ;<math>\frac{1}{e^3} \sim \frac{1}{20}</math> : an electron has 1/20 of its original energy after traveling 3 radiation lengths (3 <math>X_0</math>) through the material |
; After 2.3 radiation lengths the electron energy is down by a factor of 10 from its original value. | ; After 2.3 radiation lengths the electron energy is down by a factor of 10 from its original value. | ||
| Line 227: | Line 228: | ||
: see [http://www.nndc.bnl.gov National Nuclear Data Center]: | : see [http://www.nndc.bnl.gov National Nuclear Data Center]: | ||
| − | ; Note: Soft photons are photons created in the scattering process which have less energy than the energy of the particles participating in the interaction. Soft | + | ; Note: Soft photons are photons created in the scattering process which have less energy than the energy of the particles participating in the interaction. Soft photons are not energtic enough to be detected. |
To improve simulation speed though, GEANT 4 actually uses a fit to the above cross sections such that | To improve simulation speed though, GEANT 4 actually uses a fit to the above cross sections such that | ||
| Line 299: | Line 300: | ||
|K || 1 || <math>1S_0</math> || || 3 | |K || 1 || <math>1S_0</math> || || 3 | ||
|- | |- | ||
| − | |L || 2 || <math>2P_{3/2} , 2P_{1/2}</math> || | + | |L || 2 || <math>2P_{3/2} , 2P_{1/2}</math> || <math>3P_{3/2}</math>|| 5 |
|- | |- | ||
|} | |} | ||
| Line 306: | Line 307: | ||
{| border="3" cellpadding="20" cellspacing="0" | {| border="3" cellpadding="20" cellspacing="0" | ||
| − | | Shell || n || Spect. Notation || colspan="3"| Binding Energy (eV) | + | | Shell || n || <math>\ell</math> || m ||Spect. Notation || colspan="3"| Binding Energy (eV) |
| + | |- | ||
| + | | || <math>2n^2</math>|| || || || Measured ||GEANT4 || Moseley | ||
|- | |- | ||
| − | | || || || | + | |<math>K</math> || 1 || 0 || <math>\pm 1/2</math>|| <math>1S</math> || 3218 || 3178 || 3061 |
|- | |- | ||
| − | |<math> | + | |<math>L_{I}</math> || 2 || 0 || <math>\pm 1/2</math>||<math>2S</math> || 328 ||313.5 || 575 |
|- | |- | ||
| − | |<math>L_{ | + | |<math>L_{II}</math> || 2 || 1 || <math>\pm 1/2</math>||<math>2P_{1/2}</math> || 251 || 247 || 575 |
|- | |- | ||
| − | |<math>L_{ | + | |<math>L_{III}</math> || 2 || 1 || <math>\pm 1/2, \pm 3/2</math>||<math>2P_{3/2}</math> || 248.4|| 247 || 575 |
|- | |- | ||
| − | |<math> | + | |<math>M</math> || 3 || 1 || |
|- | |- | ||
|} | |} | ||
| Line 605: | Line 608: | ||
:Thomson & Rayleigh scattering are classical processes related to Compton scattering. | :Thomson & Rayleigh scattering are classical processes related to Compton scattering. | ||
| − | :Klein-Nishina formula reduces to the Thomson cross section at low energies such that <math>\sigma_{Thompson} = \frac{8 \pi}{3} r_e^2</math>. Thomson scattering produces polarized light because at these low non-relativistic energies the particle that absorbs the photon emits it in a direction perpendicular to its motion, that motion is the result of seeing the oscillating E & M wave from the incident photon. | + | :Klein-Nishina formula reduces to the Thomson cross section at low energies (photon Energy < < particle mass) such that <math>\sigma_{Thompson} = \frac{8 \pi}{3} r_e^2</math>. Thomson scattering produces polarized light because at these low non-relativistic energies the particle that absorbs the photon emits it in a direction perpendicular to its motion, that motion is the result of seeing the oscillating E & M wave from the incident photon. |
| − | :Rayleigh scattering (<math>\sigma_{Rayleigh} \propto \frac{1}{\lambda^4}</math>) is photon scattering from an atom as a whole, coherent scattering. No energy is transfered to the Medium in either case, <math>\gamma</math> only changes direction. Rayleigh scattering is the elastic scattering of the photon from a particle (atoms & molecule have diameters less than a nm) that is '''smaller''' than the wavelength of the light( visible light is 400 -> 700 nm) . | + | :Rayleigh scattering (<math>\sigma_{Rayleigh} \propto \frac{1}{\lambda^4}</math>) is photon scattering from an atom as a whole, coherent scattering. No energy is transfered to the Medium in either case, <math>\gamma</math> only changes direction. Rayleigh scattering is the elastic scattering of the photon from a particle (atoms & molecule have diameters less than a nm) that is '''smaller''' than the wavelength of the light( visible light is 400 -> 700 nm) . |
:Mie solution is used to describe elastic scattering of E&M waves from spheres (particles) that are '''larger''' than the wavelength of the incident photon. | :Mie solution is used to describe elastic scattering of E&M waves from spheres (particles) that are '''larger''' than the wavelength of the incident photon. | ||
| Line 767: | Line 770: | ||
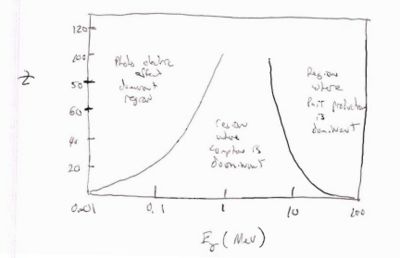
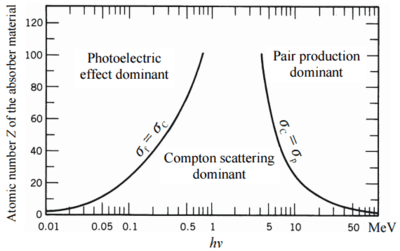
At low energy (keV), the photo-electric effect dominant while at high energies (> 1 MeV) pair production starts to dominate. Compton scattering dominates in the intermediate energy region. | At low energy (keV), the photo-electric effect dominant while at high energies (> 1 MeV) pair production starts to dominate. Compton scattering dominates in the intermediate energy region. | ||
| − | [[Image:SPIM_PhotoAbsorptionPhysicsProcess-vs-Z.jpg | 400 px]] | + | [[Image:SPIM_PhotoAbsorptionPhysicsProcess-vs-Z.jpg | 400 px]][[Image:SPIM_PhotoAbsorptionPhysicsProcess-vs-Z_a.jpg | 400 px]] |
[[Simulations_of_Particle_Interactions_with_Matter]] | [[Simulations_of_Particle_Interactions_with_Matter]] | ||
Latest revision as of 16:34, 13 April 2018
Bremsstrahlung
- Definition
- Radiation produced when a charged particle is deflected by the electric field of nuclei in a material.
- Note: There is also electron-electron brehmstrahlung but the interaction is with the electric field of the materials atomic electrons.
The Cross section formula is given in Formula 3Cs, pg 928 of reference H.W. Koch & J.W Motz, Rev. Mod. Phys., vol 31 (1959) pg 920 as
- Note
- Bethe & Heitler first calculated this radiation in 1934 which is why you will sometimes hear Bremsstrahlung radiation refererd to as Bethe-Heitler.
where
- = initial total energy of the electron
- = final total energy of the electron
- = energy of the emitted photon
- = Atomic number = number of protons in target material
- = charge screening parameter
Coulomb correction to using the Born approximation (approximation assumes the incident particle is a plane wave interacting with a static E-field, the correction accounts for changes in the plane wave due to the presence of the field). Charge screening and the coulomb correction are different effects that have been shown to be additive/independent. File:Haug 2008.pdf
- and = screening functions that depend on Z
if
For Z<5 see Tsai, Rev.Mod. Phys., vol 46 (1974) pg 815
- if use Equation 3.46 and 3.47
- if use Equation 3.25 and 3.26
- Note
- Energy loss via Bethe-Bloch is due to coulomb deflection and is a continuous process while Bremsstrahlung is a discrete process (emission of photons)
- We now know 2 ways charged particles can loose energy when passsing through matter.
- Energy loss
- : Bremsstrahlung
- : Bethe-Bloch (collision)
where
- = Energy of emmitted photon
- = Probability of Energy loss
The quantity is defined such that
is a macroscopic function of a given material rather than just the energy which we will use to define a common property of materials known as the radiation length
where
- case is no screening and
- case has
The energy loss equation becomes
- Note
- for intermediate value of you need to integrate numerically
- : Bremsstrahlung
- : Bethe-Bloch
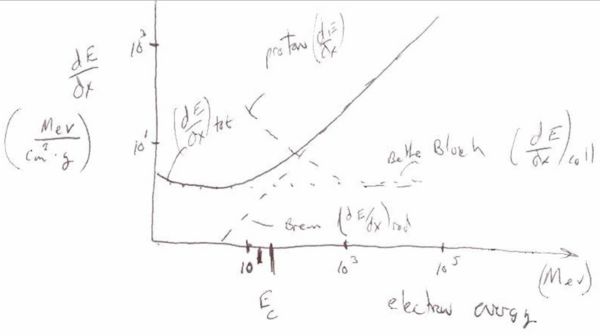
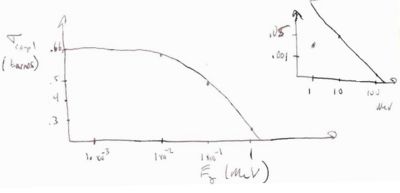
The illustration below shows the relative contributions of Bethe-Bloch and Bremsstrahlung to the total energy loss according to the above functional dependence. At low energies the physics of collisions dominates the loss (Bethe-Bloch) and as energy increases the discrete loss by radiation begins to dominate.
The energy loss, due to collisions, of a proton is overlaid for comparison.
- Critical Energy
At the critical energy the two energy loss processes contribute equally to the total energy lost by a charged particle interacting with matter.
- energy at which
In the PDG
- Examples
Critical Energy E_C | |
| Material | (MeV) |
| Pb | 9.51 |
| Fe | 27.4 |
| Cu | 24.8 |
| Al | 51 |
Electron-Electron Bremsstrahlung
- Electron electron bremsstrahlung
- The radiation produced as 2 electrons pass near eachother
- is essentially the same except you have thereby adding a term and not a term
reference:pg 947 from Koch and Motz, Rev. Mod. Phys, vol 31 (1959) pg 920 File:SPIM Koch andMotz RevModPhysv31 1959pg920.pdf
as a result
- =
Most calculations ignore electron-electron Brehmsstrahung because its linear in Z and doesn;t become important until low Z where measured atomic form factors are actually used and not Form factors calulated by the Thomas-Fermi-Moliere Model (Z>4).
Coherent Bremsstrahlung
The above equations represent the physics of incoherent bremsstrahlung production.
http://137.99.79.133/halld/tagger/references/inelasticBrems-94.pdf
Radiation Length (Xo)
- Radiation Length
- The distance an electron travels through matter until loosing of its energy due to radiation .
in the high energy limit where can be ignored
or
where
- = Radiation Length of a given material
ie:
- if Then = Energy of electron after traveling a distance of through the material
Table of Radiation Lengths for several materials | |
| Material | (cm) |
| Air | 30,050 |
| Al | 8.9 |
| Cu | 1.43 |
| Fe | 1.76 |
| H2O | 36.1 |
| NaI | 2.59 |
| Pb | 0.56 |
| Polystyrene | 42.9 |
| Scintillators | 42.2 |
- If we have complete screening
- Then
- =
where
- = radiation logarithm for elastic Atomic scattering
- = radiation logarithm for inelastic Atomic scattering
- :Z < 92
- Quick Estimates
- Examples of Radiation length
- an electron has 1/3 of its original energy after traveling 1 radiation length (1 ) through the material
- an electron has 1/7 of its original energy after traveling 2 radiation lengths (2 ) through the material
- an electron has 1/20 of its original energy after traveling 3 radiation lengths (3 ) through the material
- After 2.3 radiation lengths the electron energy is down by a factor of 10 from its original value.
Bremsstrahlung in GEANT 4
GEANT4 uses an energy cut off to decide whether to use a continuous energy loss algorithm (msc, Bethe-Bloch, soft photons) or to generate a secondary particle (photon) and use Bremsstrahliung.
- = incident particle K.E. cutof = secondary particle production threshold
- = photon energy cutoff below which photons are treated as continuous energy loss.
- if then no photon is created and the effect of the soft photon reaction is treated as a continuous energy loss via
- = continuous energy loss via "soft" photon emission
- = cross sections parametrerized by the Evaluated Electrons Data Library (EEDL)
- reference: J. Tuli, "Evaluated Nuclear Structure Data File", BNL-NCS - 51655 -Rev 87, 1987 from Brookhaven Nat. Lab
- see National Nuclear Data Center:
- Note
- Soft photons are photons created in the scattering process which have less energy than the energy of the particles participating in the interaction. Soft photons are not energtic enough to be detected.
To improve simulation speed though, GEANT 4 actually uses a fit to the above cross sections such that
where
- = electron mass
- = kinetic energy of incident particle
- = Avagadros number
- = constants
- = polynomial (in log(T) ) chosen to fit the data
- if then a photon is created and tracked
- The energy of the emitted photon is determine by sampling a probability distribution from
- S. Seltzer and M. Berger, Atomic Data & Nucle. Data tables, vol 35 (1986) pg 345-418
and
- the angular distribution () is sampled according to
- E. Acosta, Appl. Phys. Letter, vol 80 # 17 (2002) pg 3228-3230
Note
- The MC program PENELOPE was used to generate the energy distributions that are sampled
- GEANT4 uses a modified version of base equations for bremsstrahlung with model corrections for
- LPM effect
- There is also a correction kown as the Landau Pomeranchuk Migdal (LPM) effect which corrects for multiple scattering experiences by the electron during the scattering which causes the emission of a photon.
Bragg's Rule for compound materials
The radiation length for compounds and mixtures is determined by parallel weighting (resistors in parallel)
where
- = fraction , by wieght, of each element in the mixture/compound.
- = # of atoms of element "i"
- = atomic # of element "i"
- = effective atomic mass of the compound/mixture
Photo-electric effect
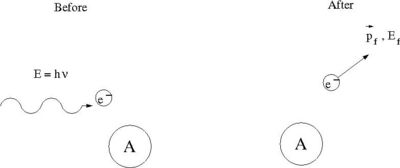
The photo-electric effect identifies the physics process by which bound electrons in an atom are liberated by an interaction with an incident photon.
where
- = incident photon energy
- = electron binding energy
Moseley's Law
Moseley's law approximates the binding energies of electrons in atoms as
- (eV)
X-ray electron shells are labeled K,L,M
| Shell | n | Spect. Notation (low E) | Spect. Notation (High E) | k_s |
| K | 1 | 3 | ||
| L | 2 | 5 |
- Example
- Binding Energies for Argon (A=18) "Chemical Rubber Company Handbook of Chemistry and Physics", CRC press. Boca Raton FL, 81st ed, 2000.
| Shell | n | m | Spect. Notation | Binding Energy (eV) | |||
| Measured | GEANT4 | Moseley | |||||
| 1 | 0 | 3218 | 3178 | 3061 | |||
| 2 | 0 | 328 | 313.5 | 575 | |||
| 2 | 1 | 251 | 247 | 575 | |||
| 2 | 1 | 248.4 | 247 | 575 | |||
| 3 | 1 | ||||||
Binding energies for a few common elements
| Element | Binding Energy (eV) | ||||
| n=1 | n=2 | n=3 | |||
| B | 201 | 14.2 | 8.3 | ||
| C | 298 | 17.9 | 11.4 | ||
| N | 450 | 26 | 15 | ||
| O | 548 | 33 | 13.6 | ||
| Na | 1083 | 71 | 38 | 5.2 | |
| Mg | 1313 | 94 | 55 | 7.7 | |
| Al | 1573 | 126 | 81 | 11 | 6 |
| Si | 1854 | 157 | 107 | 15 | 8.2 |
| P | 2167 | 195 | 141 | 20 | 10.5 |
| S | 2490 | 236 | 172 | 21.3 | 10.4 |
| Cl | 2844 | 279 | 210 | 25 | 13 |
| K | 3615 | 386 | 303 | 41 | 25 |
Photo-electric cross section
- the most general expression
where
- = scattered electron wave number [ ]
- = incident photon wave frequency
- = incident photon polarization
- = momentum given to the atom divided by Plank's constant (h)
if the electron's K.E. after emission is larger than its binding energy
then
For K shell emmission
at higher energies (the ultra-relativistic limit
References
http://physics.nist.gov/PhysRefData/Xcom/html/xcom1.html
http://www-amdis.iaea.org/LANL/
http://www.nist.gov/pml/data/ionization/index.cfm
Mass Attenuation Coefficient
The mass attenuation coefficient is used to describe the attenutation of a photon interacting with matter via the photo-electric effect ( absorption), coherent scattering (Rayleigh), incoherent scattering (Compton), or pair production.
- = linear photo-electric attenutaion
- = density of the material
The mass attenuation coefficient measures the average number of interactions between the incident photons and matter per mass unit area of traversed material thickness.
The mass energy-absorption coefficient () measures the average fraction incident photon energy transferred to the kinetic energy of the charged particles hit by the photon.
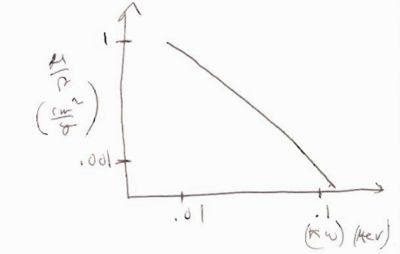
- Eample
- Below is an example of the mass atenuation coefficeint as a function of the incident photon energy
a 10 keV photon (0.01 MeV) will have when traveling through water
- = attenuation coefficient
- = intensity of light
- if
- = half length = = 0.69 cm
This means that 1/2 of the photons impinging on water get absorbed by the water atoms after a depth of 0.69 cm.
- Scaling
- Sometimes when is not available for your material you can scale a of a material with similar atomic number using the equation
where the coefficient varies with the photon energy from 4 5 according to:
GEANT4
GEANT4 uses a parameterization of photon absorption cross sections to determine the mean free path, atomic shell data to determine the ejected electron energy, and the k-shell angular distribution to determine the direction of the ejected electron.
The fit to the photoabsorption cross sections
- The photoabsorption cross section is parametrized according to
where
- are determined by a least squares fit to the data as outlined in
F. Biggs & R. Lighthill, Sandia Lab Preprint, SAND 87-0070 (1990)
File:Biggs Lighthill SandiaPreprint 87-0070.pdf
You select by sampling from a distribution generated by the above cross section.
The mean free path () of the photon through the material is given by
where
K.E. of ejected electron
Given that a photo-electric event happens then the energy of the ejected electron is given by
where
- = energy of the incident photon
- = electron shell energy from the closest available atomic shell as tabulated in data/G4EMLOW/fluor/binding.dat
The shell is selected according to the shell cross sections
Electron direction
The ejected electron is chosen by an angle according to the Souter-Gavrila distribution (Gavrila_M._Phys.Rev._vol113_1959_pg514) in the "standard" package such that
where rnd is a random number chosen such that
Physics Models
G4PhotoElectricEffect
This model will generate an ionized electron which is about the same as the incident photon energy. Don't use this one if your simulation is sensitive to atomic energy levels (ie; looking at keV energy effects). This should be O.K. if you are just interested in attenuating photons.
G4LowEnergyPhotoElectric (dropped in version 4.9)
This process will generate ionized electrons for each possible electron binding energy which is less than the incident photon energy. It should be cross section weighted.
This model seems to break when 100 keV (GEANT4 version 4.8)
PAI Model
PhotoAbsorption Ionizaton (PAI) Model
The PAI model uses a least squares fit of a 4th order polynomial in to the experimental photoabsorption data for the cross section such than
where
- = fit coefficent for energy bin
- = energy transfered in the ionization collision
Compton Scattering
Compton scattering is like the photo-electric effect except the photon isn't absorbed but scattered by atomic electrons.
"Ideal" compton scattering is described in terms of free electrons.
The collision is elastic
- = electron compton wavelength =
- = electron final kinetic energy
- = ejected electron angle w.r.t original photon direction
- Note
- : No electrons can be backscattered in the compton process.
- The photon can backscatter
- = Max energy transfered to the
- = The max energy transfer point corresponds to the "compton" edge
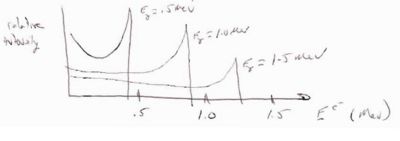
- Example
- Find of the compton edge for a given .
- If = 8 keV
- Then eV = max energy lost by photon and given to electron
Cross Section
The Klein-Nishina formula (Oskar Klein & Yoshio Nashina, Z. fur Phys., vol 52 (1929), pg 853 ) is given as
where
- Note
- The above cross section is for a free electron. Multiple by (the number of electrons in the target) to get the atomic cross section.
After integrating over
Energy Distribution
The compton electron energy distribution can be evaluated from the differential cross section below
where
- barns
- MeV
GEANT 4
GEANT 4 parametrized the Compton cross section to reproduce the data down to 10 keV using the expression
- are determined from fit
The data used in the fit may be found in
- Hubbell, Grimm, & Overbo, J. Phys. Chem. Ref. Data 9, (1980) pg 1023
- H. Storm, Nucl. Data Tables, A7 (1970) pg 565
In addition to the default and low energy models which come with GEANT4 (as was available with the Photo Electric effect), there is also a model called "G4LECS" which may be installed.
- Models
- a.) G4ComptonScattering: listed as "compt" in the process name. No Rayleigh scattering in the model.
- b.) G4LowEnergyCompton: Process name is "LowEnCompton" in the tracking code. It has errors in the treatment of Rayleigh scattering and does not account for doppler broadening (the effect of bound electron momentum on the scattered particle energies).
- c.) G4LECS: Bound electron effects are corrected for on an :shell-by-shell" basis. Rayleigh scattering is modeled using the coherent scattering cross section and form factor data. The Doppler broadening effect is included ( a result of the compton telescope simulation work).
- Note
- Thomson & Rayleigh scattering are classical processes related to Compton scattering.
- Klein-Nishina formula reduces to the Thomson cross section at low energies (photon Energy < < particle mass) such that . Thomson scattering produces polarized light because at these low non-relativistic energies the particle that absorbs the photon emits it in a direction perpendicular to its motion, that motion is the result of seeing the oscillating E & M wave from the incident photon.
- Rayleigh scattering () is photon scattering from an atom as a whole, coherent scattering. No energy is transfered to the Medium in either case, only changes direction. Rayleigh scattering is the elastic scattering of the photon from a particle (atoms & molecule have diameters less than a nm) that is smaller than the wavelength of the light( visible light is 400 -> 700 nm) .
- Mie solution is used to describe elastic scattering of E&M waves from spheres (particles) that are larger than the wavelength of the incident photon.
Pair Production
Pair production is similar to the Bremsstrahlung process.
Remember, in Bremsstrahlung the incident charged particle interacts with the of the Nucleus (or shell electron)
In pair production a photon interacts with the of the Nucleus.
when the recoil of the atom is taken into account
- = Threshold energy for pair production from an atom of mass
- Note
- You can also have photon-electron pair production analogous to electron-electron bremsstrahlung production.
Pair Production Cross Section
The pair production cross section is given by Equation 6.35 in (Bethe, Phys. Rev., vol. 93 (1964) pg 768)
at small angles
A version which assumes small angles is given in Eq 7.35 of the same reference as the triple differential cross section:
where
- photon momentum/energy
- = scattering angle of
- = scattering angle of
- angle between the and pair
- = Energy of the positron
- = Energy of the electron
- Note
- The above equations for the differential cross section are using "natural" units where
Davies' version integrates over all angles
Davies published a version which has been integrated over angles and includes some screening effects ( see Eq 35):
where
If you integrate over all positron ( ) energies you get Eq. 44 (no screening)
and Eq. 45 (complete screening)
Davies expressions were shown to work well at high energies ( MeV)
Overbo's low energy Cross sections
At low energies ( MeV), Overbo published an exact calculation in the case that the Atomic field is unscreened. Overbo then provided a fit to the results of his calculation which he claims is valid to within 0.1% for the energy range . The fit is given in Eq. 7.1 of his paper as
where
- Low Energy unscreened Born approximation total cross section for pair production
- = incident photon energy in units of the electron rest mass energy
Intermediate Energy Cross sections
For the Gradstein semi-ephirical formula is used from G. White Gradstein, Natl. Bur. Standard., Circ 583 (1957) pg 1.
where
- = empirical constant = 4.02 barns for Pb
- = empirical constant = 16.8 barns for Pb
- = Simulations_of_Particle_Interactions_with_Matter#Bremsstrahlung Bethe-Heitler cross section
Triplet production
- Triplet Production
- identifies photon-electron pair production. The recoiling electron track adds to the two tracks making three total particle tracks (kind of like pair production ionization).
A description for how to calculate the cross section for this process is illustrated for 1 in L.E. Wright, Phys. Rev. C 36 (1987) pg 582. Unfortunately, analytic expression is not given but one could construct tables of and in equation 65 of L.E. Wright's paper.
An example for may be found in Sud & Vargus, Phys. Rev. A49 (1994) pg 4624.
GEANT4 Pair production
GEANT4 uses the pair production cross section given in Tsai, Rev. Mod. Phys, vol 46 (1974) pg 815.
where
- energy of incident photon
- KE of create electron
- fraction of taken away by
- triplet production correction
- high energy coulomb correction from Davies above
- & = electron screening functions
The formula GEANT4 uses may also be found on pg 541 in J. Bono , Radiation Physics Chemistry, vol 44 (1994) pg 531
where
- = low energy coulomb correction
- = screening radius (adjustable parameter)
- = Compton wavelength
An older simulation description with graphs of the cross-sections may be found below.
File:Bigg Lighthill conversion 1Mev-100MeV SandiaPreprint SC-RR-68-619.pdf
Below is the review of Modern Physics article basically summarizing all of the physics for pair production up to 1969
File:RevModPhys PairPoduction 1969 MotzOlsonKoch.pdf
Contributions as function of Z
The plot below shows the contributions of the three photon absorption physics processes as a function of the incident photon energy and the Z of the target material. At low energy (keV), the photo-electric effect dominant while at high energies (> 1 MeV) pair production starts to dominate. Compton scattering dominates in the intermediate energy region.