Difference between revisions of "2NCorr SPDP Introduction"
| Line 13: | Line 13: | ||
==two-neutron opening angle== | ==two-neutron opening angle== | ||
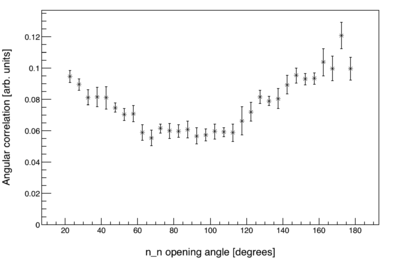
| − | For <math>\theta_{nn}</math>, the control distribution is made by looking at the events from pairs of two pulses, such that the the two pulses occurred within a few 100 ms of each other. If there is a neutron event in both of the pulses from a given pulse pair, then the opening angle between the two events is calculated. Since no information can be shared between the neutrons of different pulses, the control distribution must be free of any two-neutron correlations. However, the control distribution is still subject to the exact same effects of detector geometry and efficiency as the distribution from truly correlated neutron pairs. So what is meant by "angular correlation" here, is the measured rate relative to a totally uncorrelated neutron source. The plot below is the same data from the plot above, but after normalization to an uncorrelated source. | + | For <math>\theta_{nn}</math>, the control distribution is made by looking at the events from pairs of two pulses, such that the the two pulses occurred within a few 100 ms of each other. If there is a neutron event in both of the pulses from a given pulse pair, then the opening angle between the two events is calculated. Since no information can be shared between the neutrons of different pulses, the control distribution must be free of any two-neutron correlations. However, the control distribution is still subject to the exact same effects of detector geometry and efficiency as the distribution from truly correlated neutron pairs. So what is meant by "angular correlation" here, is the measured <math>\theta_{nn}</math> rate relative to a totally uncorrelated neutron source. The plot below is the same data from the plot above, but after normalization to an uncorrelated source. |
<div><ul> | <div><ul> | ||
Revision as of 00:01, 20 January 2018
The calculation of angular correlation
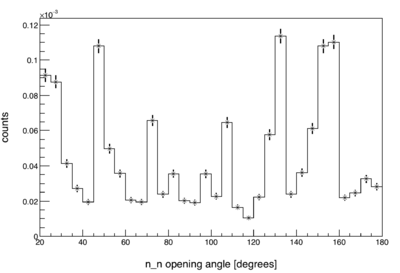
The neutron efficiency and acceptance of our detector array varies highly non-uniformly over the range of two-neutron opening angles (). This is due to the detector array's non-spherically symmetric geometry, and to its varying neutron detection efficiency as a function of both position and energy (see figure).
For this reason, every measured distribution is made meaningful by normalizing against a "control" distribution. This is done by diving the values of the measured distribution by the control distribution on a bin-by-bin basis.
two-neutron opening angle
For , the control distribution is made by looking at the events from pairs of two pulses, such that the the two pulses occurred within a few 100 ms of each other. If there is a neutron event in both of the pulses from a given pulse pair, then the opening angle between the two events is calculated. Since no information can be shared between the neutrons of different pulses, the control distribution must be free of any two-neutron correlations. However, the control distribution is still subject to the exact same effects of detector geometry and efficiency as the distribution from truly correlated neutron pairs. So what is meant by "angular correlation" here, is the measured rate relative to a totally uncorrelated neutron source. The plot below is the same data from the plot above, but after normalization to an uncorrelated source.