Difference between revisions of "LB 170063 Nickel Information With Dead Time"
Jump to navigation
Jump to search
| (25 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | Below is a table with thin windows, original windows, and expanded windows for the nickel on sample 170063 | + | Below is a table with thin windows, original windows, and expanded windows for the nickel on sample 170063. The thin window method can be found at [[LB Thesis Thin Window Analysis]]. |
| − | |||
{| border="3" cellpadding="5" cellspacing="0" | {| border="3" cellpadding="5" cellspacing="0" | ||
|| || 5/25/17 || 5/26/17 || 5/27/17|| 5/29/17 || 5/30/17 || 5/31/17 || 6/1/17 || | || || 5/25/17 || 5/26/17 || 5/27/17|| 5/29/17 || 5/30/17 || 5/31/17 || 6/1/17 || | ||
| Line 26: | Line 25: | ||
||Runtime (s) || 301.337 || 301.322 || 327.734 || 300.228 || 272.845 || 300.691 || 306.858 | ||Runtime (s) || 301.337 || 301.322 || 327.734 || 300.228 || 272.845 || 300.691 || 306.858 | ||
|- | |- | ||
| − | ||Rate (Hz) || <math> 1.009048 \times 10^6 \pm 1.2829 \times 10^4 </math> || <math>7.58401 \times 10^5 \pm 2.470 \times 10^3</math> ||<math> 4.15280 \times 10^5 \pm 1.248 \times 10^3 </math> || | + | ||Rate (Hz) || <math> 1.009048 \times 10^6 \pm 1.2829 \times 10^4 </math> || <math>7.58401 \times 10^5 \pm 2.470 \times 10^3</math> ||<math> 4.15280 \times 10^5 \pm 1.248 \times 10^3 </math> || <math>1.84531 \times 10^5 \pm 8.58 \times 10^2 </math>||<math> 8.4720 \times 10^4 \pm 3.2115 \times 10^2</math> ||<math> 5.8017 \times 10^4 \pm 2.5233 \times 10^2 </math>|| <math> 3.5402 \times 10^4 \pm 1.9360 \times 10^2 </math> |
| + | |- | ||
| + | ||True Rate (Integral Method) (Hz) || <math>1.040020 \times 10^6 \pm 1.3222 \times 10^4 </math> ||<math> 7.81679 \times 10^5 \pm 2.5458 \times 10^3</math> ||<math> 4.29155 \times 10^5 \pm 1.290 \times 10^3 </math> || <math> 1.90175 \times 10^5 \pm 8.8425 \times 10^2 </math>||<math> 8.7072 \times 10^4 \pm 3.29 \times 10^2 </math> || <math> 5.9793 \times 10^4 \pm 2.59 \times 10^2 </math> || <math> 3.6508 \times 10^4 \pm 2.00 \times 10^2 </math> | ||
| + | |- | ||
| + | ||Number of Entries in Histogram || 566090 || 1015134 || 1428804 || 541498 || 984165 || 761238 ||494039 | ||
| + | |- | ||
| + | ||<math> \frac{Entries}{Runtime} </math> || 1878.59 || 3368.93 || 4359.64 || 1803.62 || 3607.05 || 2531.63 || 1609.99 | ||
| + | |- | ||
| + | || Percent Dead ||3.95 +/- 0.42 || 6.59 +/- 0.43 || 9.09 +/- 0.60 || 3.95 +/- 0.42 || 6.59 +/- 0.43 || 5.06 +/- 0.39 || 3.06 +/- 0.3 | ||
| + | |- | ||
| + | ||True Rate (Hz) || <math> 1.082790 \times 10^6 \pm 1.4557 \times 10^4 </math> || <math> 8.36825 \times 10^5 \pm 4.764 \times 10^3 </math> || <math> 4.72065 \times 10^5 \pm 3.332 \times 10^3</math> || <math> 1.97995 \times 10^5 \pm 1.322 \times 10^3</math> || <math> 9.3214 \times 10^4 \pm 5.59 \times 10^2</math> || <math> 6.2979 \times 10^4 \pm 3.62 \times 10^2 </math> ||<math> 3.7660 \times 10^4 \pm 2.33 \times 10^2 </math> | ||
| + | |- | ||
| + | ||Backtracked Signal (For Consistency) || || | ||
| + | |- | ||
| + | ||.dat file entry || 13.90 +/- 0.01 || 13.64 +/- 0.01 || 13.06 +/- 0.01 || 12.20 +/- 0.01 || 11.44 +/- 0.01 || 11.04 +/- 0.01|| 10.54 +/- 0.01 | ||
|- | |- | ||
|} | |} | ||
| + | |||
| + | We can also trace these signals back in time to make sure that they somewhat match up with the previous signal that was seen. | ||
| + | |||
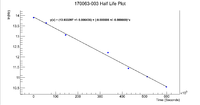
| + | Below is a plot that was made to help find the half life and the initial activity of the sample | ||
| + | |||
| + | [[File:170063 NickelFoil HLPlot DeadTimeCorrected.png|200px]] | ||
| + | |||
| + | from here we can see that | ||
| + | |||
| + | <math> Slope = 5.63921 \times 10^{-6} \pm 1.75557 \times 10^{-8} </math> | ||
| + | |||
| + | and the intercept is given by | ||
| + | |||
| + | <math> 13.9333 \pm 0.00643596 </math> | ||
| + | |||
| + | By exponentiating the intercept, we can find the activity of the nickel foil at the time of the first measurement, which is | ||
| + | |||
| + | <math> 1.125007 \times 10^6 \pm 7.240 \times 10^3 </math> | ||
| + | |||
| + | Now note that this measurement was taken 8 minutes after the selenium samples were measured. So we must correct the activity back 8 minutes. | ||
| + | |||
| + | <math> A_0 = 1.125007 \times 10^6 \times e^{5.40845 \times 10^{-6} \times 480} = 1.127931 \times 10^6 Hz </math> | ||
| + | |||
| + | <math> \sigma_{A_0} = 7240 \times e^{5.40845 \times 10^{-6} \times 480} = 7258.82 Hz </math> | ||
Latest revision as of 22:02, 6 December 2017
Below is a table with thin windows, original windows, and expanded windows for the nickel on sample 170063. The thin window method can be found at LB Thesis Thin Window Analysis.
We can also trace these signals back in time to make sure that they somewhat match up with the previous signal that was seen.
Below is a plot that was made to help find the half life and the initial activity of the sample
from here we can see that
and the intercept is given by
By exponentiating the intercept, we can find the activity of the nickel foil at the time of the first measurement, which is
Now note that this measurement was taken 8 minutes after the selenium samples were measured. So we must correct the activity back 8 minutes.