Difference between revisions of "JB Absolute theta"
Jump to navigation
Jump to search
| Line 9: | Line 9: | ||
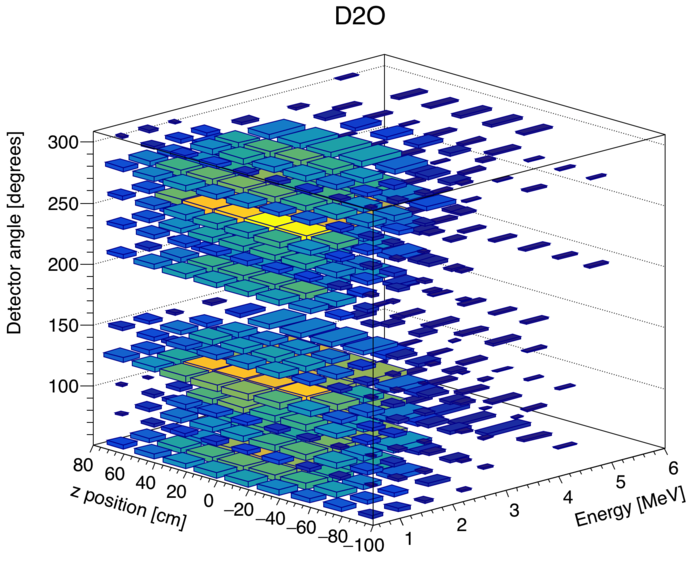
[[File:D2O3DHistogram.png|700px|thumb|center|alt=Large | Every singles event lies in a three dimensional space consisting of a PMT top and bottom time, and a specific detector. These observables can be recast as energy, vertical z position, and detector angle (54,78,102, ect). ]] | [[File:D2O3DHistogram.png|700px|thumb|center|alt=Large | Every singles event lies in a three dimensional space consisting of a PMT top and bottom time, and a specific detector. These observables can be recast as energy, vertical z position, and detector angle (54,78,102, ect). ]] | ||
| − | The benefit of conducting the analysis in this 3D space, is that the photo-neutrons correlated with the beam can be normalized to uncorrelated Cf252 neutrons detected in the same detector | + | The benefit of conducting the analysis in this 3D space, is that the photo-neutrons correlated with the beam can be normalized to uncorrelated Cf252 neutrons detected in the same detector with similar positions and energies. |
Revision as of 21:50, 10 November 2017
Analysis
After my first attempt at reconstructing the theta_abs distribution gave mediocre results, I decided to try again, but this time without integrating over experimental observables throught analysis, except for at the final step. To illustrate what I mean, see the histogram below:
The benefit of conducting the analysis in this 3D space, is that the photo-neutrons correlated with the beam can be normalized to uncorrelated Cf252 neutrons detected in the same detector with similar positions and energies.