Initial CM Frame 4-momentum components

[math]\textbf{\underline{Navigation}}[/math]

[math]\vartriangleleft [/math] [math]\triangle [/math] [math]\vartriangleright [/math]

Initial CM Frame 4-momentum components

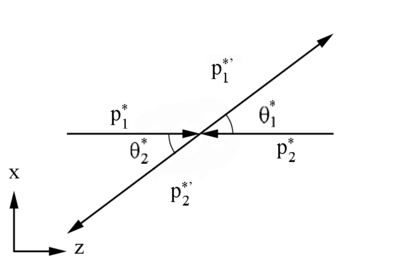
Figure 2: Definition of variables in the Center of Mass Frame

Starting with the definition for the total relativistic energy:

[math]E^2\equiv p^2c^2+m^2c^4[/math]

[math]\Longrightarrow {E^2}-p^2c^2=(mc^2)^2[/math]

Since we can assume that the frame of reference is an inertial frame, it moves at a constant velocity, the mass should remain constant.

[math]\frac {d\vec p}{dt}=0\Rightarrow \frac{d(m\vec v)}{dt}=\frac{v\ dm}{dt}\Rightarrow \frac{dm}{dt}=0[/math]

[math] \therefore m=const[/math]

We can use 4-momenta vectors, i.e. [math]{\mathbf P}\equiv \left(\begin{matrix} E\\ p_x \\ p_y \\ p_z \end{matrix} \right)=\left(\begin{matrix} E\\ \vec p \end{matrix} \right)[/math] ,with c=1, to describe the variables in the CM Frame.

Using the fact that the scalar product of a 4-momenta with itself,

[math]{\mathbf P_1}\cdot {\mathbf P^1}=P_{\mu}g_{\mu \nu}P^{\nu}=\left(\begin{matrix} E\\ p_x \\ p_y \\ p_z \end{matrix} \right)\cdot \left( \begin{matrix}1 & 0 & 0 & 0\\0 & -1 & 0 & 0\\0 & 0 & -1 & 0\\0 &0 & 0 &-1\end{matrix} \right)\cdot \left(\begin{matrix} E & p_x & p_y & p_z \end{matrix} \right)[/math]

[math]{\mathbf P_1}\cdot {\mathbf P^1}=E_1E_1-\vec p_1\cdot \vec p_1 =m_{1}^2=\sqrt{s}[/math]

is invariant.

Using this notation, the sum of two 4-momenta forms a 4-vector as well

[math]{\mathbf P_1}+ {\mathbf P_2}= \left( \begin{matrix}E_1+E_2\\\vec p_1 +\vec p_2 \end{matrix} \right)= {\mathbf P}[/math]

The length of this four-vector is an invariant as well

[math]{\mathbf P^2}=({\mathbf P_1}+{\mathbf P_2})^2=(E_1+E_2)^2-(\vec p_1 +\vec p_2 )^2=(m_1+m_2)^2=s[/math]