Difference between revisions of "Initial CM Frame 4-momentum components"
Jump to navigation
Jump to search
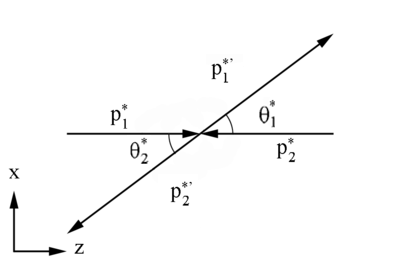
Figure 2: Definition of variables in the Center of Mass Frame
(Created page with "=Initial CM Frame 4-momentum components= <center>400 px</center> <center>'''Figure 2: Definition of variables in the Center of Mass Frame'''</center> …") |
|||
| Line 33: | Line 33: | ||
| − | <center><math>{\mathbf P_1}\cdot {\mathbf P^1}=E_1E_1-\vec p_1\cdot \vec p_1 =m_{1}^2 | + | <center><math>{\mathbf P_1}\cdot {\mathbf P^1}=E_1E_1-\vec p_1\cdot \vec p_1 =m_{1}^2</math></center> |
Revision as of 02:14, 14 June 2017
Initial CM Frame 4-momentum components

Starting with the definition for the total relativistic energy:
Since we can assume that the frame of reference is an inertial frame, it moves at a constant velocity, the mass should remain constant.
We can use 4-momenta vectors, i.e. ,with c=1, to describe the variables in the CM Frame.
Using the fact that the scalar product of a 4-momenta with itself,
is invariant.
Using this notation, the sum of two 4-momenta forms a 4-vector as well
The length of this four-vector is an invariant as well