Relativistic Frames of Reference

[math]\textbf{\underline{Navigation}}[/math]

[math]\vartriangleleft [/math] [math]\triangle [/math] [math]\vartriangleright [/math]

Relativistic Frames of Reference

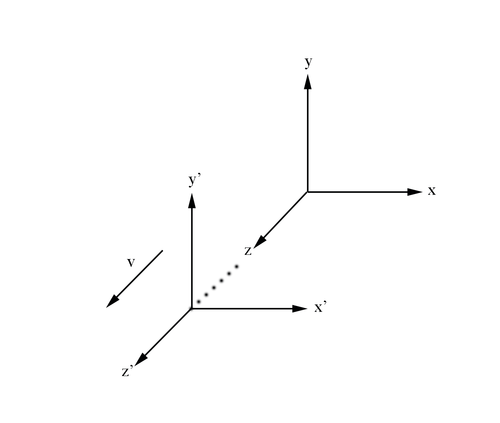
From the Galilean description of motion for a frame of reference moving relative to another frame considered stationary we know that

Figure 2.1: Primed reference frame moving in the z direction with velocity v.

In the rest frame of v=0

[math]\begin{cases} t= t' \\ x=x' \\ y=y' \\ z=z'+vt' \end{cases}[/math]

Using Einstein's Theory of Relativity, we know that the speed of light is a constant, c, for all reference frames. In the unprimed frame, from the definition of speed:

[math]speed=\frac{\Delta Distance}{\Delta Time}[/math]

[math]c=\frac{\Delta d}{\Delta t}[/math]

where

[math]c=3\times 10^8\ m/s[/math]

Using the distance equation in a Cartesian coordinate system, the equation for the speed of light becomes

[math]c=\frac{\sqrt{\Delta x^2+\Delta y^2+\Delta z^2}}{t}[/math]

Following the postulate of Special Relativity, this implies for the primed frame

[math]c=\frac{\sqrt{\Delta x^{'2}+\Delta y^{'2}+\Delta z^{'2}}}{t}[/math]

We can rewrite this as

[math]\frac{\Delta x^{'2}+\Delta y^{'2}+\Delta z^{'2}}{\Delta t^{'2}}= c^2=\frac{\Delta x^2+\Delta y^2+\Delta z^2}{\Delta t^2}[/math]

This is possible since the ratios of distance to time are multiples of the same base, i.e. the square of the speed of light [math](\frac{3\times 10^8\ m}{s})^2[/math]. Therefore for the relative change in the time in one frame, the distance must change by the same factor to maintain the same constant. With this we can write

[math]c^2 \Delta t^{'2}=\Delta x^{'2}+\Delta y^{'2}+\Delta z^{'2}\ \ \ \ \ c^2 \Delta t^{2}=\Delta x^2+\Delta y^2+\Delta z^2[/math]

[math]\Rightarrow c^2 \Delta t^{'2}-\Delta x^{'2}-\Delta y^{'2}-\Delta z^{'2}= c^2 \Delta t^{2}-\Delta x^2-\Delta y^2-\Delta z^2[/math]

This quantity is known as the time space interval [math]ds^2[/math] when the change is infinitesimal

[math]s^2\equiv c^2 dt^{'2}-dx^{'2}-dy^{'2}-dz^{'2}= c^2 dt^{2}-dx^2-dy^2-dz^2[/math]

Since the speed of light is a constant for all frames of reference, this allows the space time interval to also be invariant for inertial frames.

[math]s^2\equiv c^2 dt^{'2}-dx^{'2}-dy^{'2}-dz^{'2}= c^2 dt^{2}-dx^2-dy^2-dz^2[/math]

[math]s^2\equiv c^2 dt^{'2}-dr^{'2}= c^2 dt^{2}-dr^2[/math]

[math]s^2\equiv (c^2 -v^{'2})dt^{'2}= (c^2 -v^2)dt^{2}[/math]

From the rest frame of v'=0

[math]s^2\equiv c^2 dt^{'2}= (c^2 -v^2)dt^{2}[/math]

[math]\Rightarrow dt^{'2}= (1-\frac{v^2}{c^2 })dt^{2}[/math]

[math]\Rightarrow \begin{cases} dt'= \sqrt{1-\frac{v^2}{c^2 }}dt=\frac{1}{\gamma} dt\\ \\ dt= \frac{1}{\sqrt{1-\frac{v^2}{c^2 }}}dt'=\gamma dt' \end{cases}[/math]

[math]\Rightarrow \begin{cases} t'=\frac{1}{\gamma} t\\ \\ t=\gamma t' \end{cases}[/math]

Assuming motion is only along the z direction

[math]z \equiv ct\ \ \ \ z'\equiv ct'[/math]

Substituting these changes into the Galilean transformations

[math]\underline{\textbf{Galilean\ Transformations}}\quad \underline{\textbf{Lorentz\ Transformations}}[/math] [math] \begin{cases} t= t' \\ x=x' \\ y=y' \\ z=z'+vt' \end{cases} \qquad \Rightarrow \qquad \quad \begin{cases} t=\gamma (t'+vz'/c^2) \\ x=x' \\ y=y' \\ z=\gamma (z'+vt') \end{cases} [/math] [math] \begin{cases} t'= t' \\ x'=x' \\ y'=y' \\ z'=z-vt \end{cases} \qquad \Rightarrow \qquad \quad \begin{cases} t'=\gamma (t-vz/c^2) \\ x'=x' \\ y'=y' \\ z'=\gamma (z-vt) \end{cases} [/math]

---

[math]\textbf{\underline{Navigation}}[/math]

[math]\vartriangleleft [/math] [math]\triangle [/math] [math]\vartriangleright [/math]