|
|
| Line 17: |
Line 17: |
| | | | |
| | | | |
| − | In the rest frame of v'=0 | + | In the rest frame of v=0 |
| | | | |
| | <center><math>\begin{cases} | | <center><math>\begin{cases} |
Revision as of 04:21, 4 June 2017
[math]\textbf{\underline{Navigation}}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]
Relativistic Frames of Reference
From the Galilean description of motion for a frame of reference moving relative to another frame considered stationary we know that
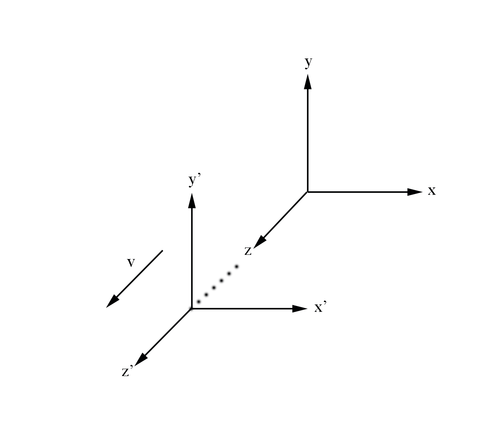
Figure 2.1: Primed reference frame moving in the z direction with velocity v.
In the rest frame of v=0
[math]\begin{cases}
t= t' \\
x=x' \\
y=y' \\
z=z'+vt'
\end{cases}[/math]
Using Einstein's Theory of Relativity, we know that the speed of light is a constant, c, for all reference frames. In the unprimed frame, from the definition of speed:
[math]speed=\frac{\Delta Distance}{\Delta Time}[/math]
[math]c=\frac{\Delta d}{\Delta t}[/math]
where
[math]c=3\times 10^8\ m/s[/math]
Using the distance equation in a Cartesian coordinate system, the equation for the speed of light becomes
[math]c=\frac{\sqrt{\Delta x^2+\Delta y^2+\Delta z^2}}{t}[/math]
Following the postulate of Special Relativity, this implies for the primed frame
[math]c=\frac{\sqrt{\Delta x^{'2}+\Delta y^{'2}+\Delta z^{'2}}}{t}[/math]
We can rewrite this as
[math]\frac{\Delta x^{'2}+\Delta y^{'2}+\Delta z^{'2}}{\Delta t^{'2}}= c^2=\frac{\Delta x^2+\Delta y^2+\Delta z^2}{\Delta t^2}[/math]
This is possible since the ratios of distance to time are multiples of the same base, i.e. the square of the speed of light [math](\frac{3\times 10^8\ m}{s})^2[/math]. Therefore for the relative change in the time in one frame, the distance must change by the same factor to maintain the same constant. With this we can write
[math]c^2 \Delta t^{'2}=\Delta x^{'2}+\Delta y^{'2}+\Delta z^{'2}\ \ \ \ \ c^2 \Delta t^{2}=\Delta x^2+\Delta y^2+\Delta z^2[/math]
[math]\Rightarrow c^2 \Delta t^{'2}-\Delta x^{'2}-\Delta y^{'2}-\Delta z^{'2}= c^2 \Delta t^{2}-\Delta x^2-\Delta y^2-\Delta z^2[/math]
This quantity is known as the time space interval [math]ds^2[/math] when the change is infinitesimal
[math]s^2\equiv c^2 dt^{'2}-dx^{'2}-dy^{'2}-dz^{'2}= c^2 dt^{2}-dx^2-dy^2-dz^2[/math]
Since the speed of light is a constant for all frames of reference, this allows the space time interval to also be invariant for inertial frames.
[math]s^2\equiv c^2 dt^{'2}-dx^{'2}-dy^{'2}-dz^{'2}= c^2 dt^{2}-dx^2-dy^2-dz^2[/math]
[math]s^2\equiv c^2 dt^{'2}-dr^{'2}= c^2 dt^{2}-dr^2[/math]
[math]s^2\equiv (c^2 -v^{'2})dt^{'2}= (c^2 -v^2)dt^{2}[/math]
From the rest frame of v'=0
[math]s^2\equiv c^2 dt^{'2}= (c^2 -v^2)dt^{2}[/math]
[math]\Rightarrow dt^{'2}= (1-\frac{v^2}{c^2 })dt^{2}[/math]
[math]\Rightarrow \begin{cases}
dt'= \sqrt{1-\frac{v^2}{c^2 }}dt=\frac{1}{\gamma} dt\\
\\
dt= \frac{1}{\sqrt{1-\frac{v^2}{c^2 }}}dt'=\gamma dt'
\end{cases}[/math]
[math]\Rightarrow \begin{cases}
t'=\frac{1}{\gamma} t\\
\\
t=\gamma t'
\end{cases}[/math]
Assuming motion is only along the z direction
[math]z \equiv ct\ \ \ \ z'\equiv ct'[/math]
Substituting these changes into the Galilean transformations
[math]\underline{\textbf{Galilean\ Transformations}}\quad \underline{\textbf{Lorentz\ Transformations}}[/math]
[math]
\begin{cases}
t= t' \\
x=x' \\
y=y' \\
z=z'+vt'
\end{cases}
\qquad \Rightarrow \qquad \quad
\begin{cases}
t=\gamma (t'+vz'/c^2) \\
x=x' \\
y=y' \\
z=\gamma (z'+vt')
\end{cases}
[/math]
[math]\textbf{\underline{Navigation}}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]
