Relativistic Frames of Reference

[math]\textbf{\underline{Navigation}}[/math]

[math]\vartriangleleft [/math] [math]\triangle [/math] [math]\vartriangleright [/math]

Relativistic Frames of Reference

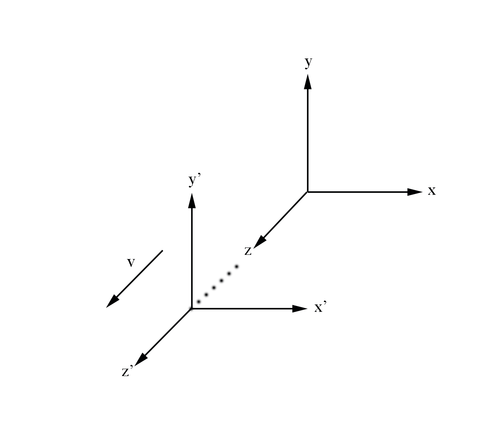
From the Galilean description of motion for a frame of reference moving relative to another frame considered stationary we know that

Figure 2.1: Primed reference frame moving in the z direction with velocity v.

[math]t= t'[/math] [math]x=x'[/math] [math]y=y'[/math] [math]z=z'+vt[/math]

Using Einstein's Theory of Relativity, we know that the speed of light is a constant, c, for all reference frames. In the unprimed frame, from the definition of speed:

[math]speed=\frac{\Delta Distance}{\Delta Time}[/math]

[math]c=\frac{\Delta d}{\Delta t}[/math]

where

[math]c=3\times 10^8\ m/s[/math]

Using the distance equation in a Cartesian coordinate system, the equation for the speed of light becomes

[math]c=\frac{\sqrt{(\Delta x)^2+(\Delta y)^2+(\Delta z)^2}}{\Delta t}[/math]

Following the postulate of Special Relativity, this implies for the primed frame

[math]c=\frac{\sqrt{(\Delta x')^2+(\Delta y')^2+(\Delta z')^2}}{\Delta t'}[/math]

We can rewrite this as

[math]c^2=\frac{(\Delta x')^2+(\Delta y')^2+(\Delta z')^2}{(\Delta t')^2}\ \ \ \ \ c^2=\frac{(\Delta x)^2+(\Delta y)^2+(\Delta z)^2}{(\Delta t)^2}[/math]

[math]c^2 \Delta t^{'2}=(\Delta x')^2+(\Delta y')^2+(\Delta z')^2\ \ \ \ \ c^2 \Delta t^{2}=(\Delta x)^2+(\Delta y)^2+(\Delta z)^2[/math]

---

[math]\textbf{\underline{Navigation}}[/math]

[math]\vartriangleleft [/math] [math]\triangle [/math] [math]\vartriangleright [/math]