|
|
| Line 138: |
Line 138: |
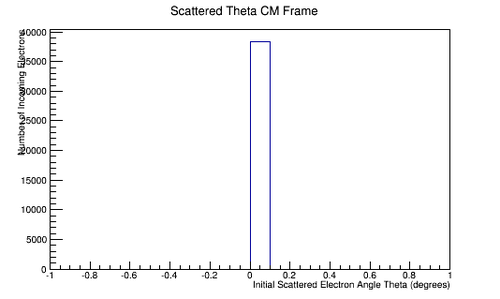
| | File:Init_e_Theta_CM.png|'''Figure 5.1.5:''' Initial incoming angle theta for a lab frame electron incident at 11GeV as seen in the center of mass frame. | | File:Init_e_Theta_CM.png|'''Figure 5.1.5:''' Initial incoming angle theta for a lab frame electron incident at 11GeV as seen in the center of mass frame. |
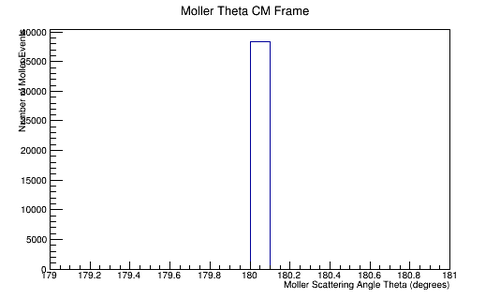
| | File:Init_Mol_Theta_CM.png|'''Figure 5.1.6:''' Initial incoming angle theta for a lab frame stationary electron as seen in the center of mass frame. | | File:Init_Mol_Theta_CM.png|'''Figure 5.1.6:''' Initial incoming angle theta for a lab frame stationary electron as seen in the center of mass frame. |
| − | | + | </gallery></center> |
| | | | |
| | | | |
Latest revision as of 18:36, 30 May 2017
[math]\textbf{\underline{Navigation}}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]
4.1.1 Center of Mass for Stationary Target
For an incoming electron of 11GeV striking a stationary electron we would expect:
Inspecting the Lorentz transformation to the Center of Mass frame:
[math]\left( \begin{matrix}E^*_{1}+E^*_{2}\\ 0 \\ 0 \\ 0\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^* \gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E_{1}+E_{2}\\ 0 \\ 0 \\ p_{1(z)}+p_{2(z)}\end{matrix} \right)[/math]
For the case of a stationary electron, this simplifies to:
[math]\left( \begin{matrix} E^* \\ p^*_{x} \\ p^*_{y} \\ p^*_{z}\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^*\gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E_{1}+m\\ 0 \\ 0 \\ p_{1(z)}+0\end{matrix} \right)[/math]
which gives,
[math]\Longrightarrow\begin{cases}
E^*=\gamma^* (E_{1}+m)-\beta^* \gamma^* p_{1(z)} \\
p^*_{z}=-\beta^* \gamma^*(E_{1}+m)+\gamma^* p_{1(z)}
\end{cases}[/math]
Solving for [math]\beta^*[/math], with [math]p^*_{z}=0[/math]
[math]\Longrightarrow \beta^* \gamma^*(E_{1}+m)=\gamma^* p_{1(z)}[/math]
| [math]\Longrightarrow \beta^*=\frac{p_{1}}{(E_{1}+m)}[/math]
|
Similarly, solving for [math]\gamma^*[/math] by substituting in [math]\beta^*[/math]
[math]E^*=\gamma^* (E_{1}+m)-\frac{p_{1}}{(E_{1}+m)} \gamma^* p_{1(z)}[/math]
[math]E^*=\gamma^* \frac{(E_{1}+m)^2}{(E_{1}+m)}-\gamma^*\frac{(p_{1(z)})^2}{(E_{1}+m)}[/math]
Using the fact that [math]E^*=[(E_{1}+E_{2})^2-(\vec p_{1}+\vec p_{2})^2]^{1/2}[/math]
[math]E^*=\gamma^* \frac{E^*\ ^2}{(E_{1}+m)}[/math]
| [math]\Longrightarrow \gamma^*=\frac{(E_1+m)} {E^*}[/math]
|
Using the relation
[math]\left( \begin{matrix} E^*_{1}+E^*_{2} \\ p^*_{1(x)}+p^*_{2(x)} \\ p^*_{1(y)}+p^*_{2(y)} \\ p^*_{1(z)}+p^*_{2(z)}\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^* \gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E_{1}+m\\ 0 \\ 0 \\ p_{1(z)}+0\end{matrix} \right)[/math]
[math]\Longrightarrow \left( \begin{matrix} E^*_{2} \\ p^*_{2(x)} \\ p^*_{2(y)} \\ p^*_{2(z)}\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^* \gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}m\\ 0 \\ 0 \\ 0\end{matrix} \right)[/math]
[math]\Longrightarrow\begin{cases}
E^*_{2}=\gamma^* (m) \\
p^*_{2(z)}=-\beta^* \gamma^* (m)
\end{cases}[/math]
[math]\Longrightarrow\begin{cases}
E^*_{2}=\frac{(E_{1}+m)}{E^*} (m) \\
p^*_{2(z)}=-\frac{p_{1}}{(E_{1}+m)} \frac{(E_{1}+m)}{E^*} (m_{2})
\end{cases}[/math]
[math]\Longrightarrow\begin{cases}
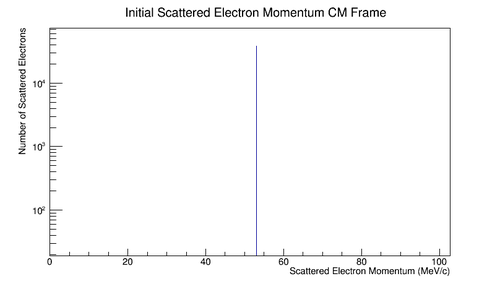
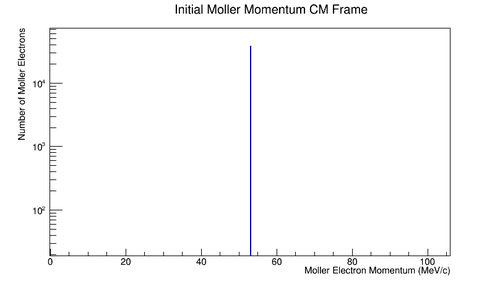
E^*_{2}=\frac{(11000 MeV+.511 MeV)}{106.031 MeV} (.511 MeV) \approx 53.015 MeV\\
p^*_{2(z)}=-\frac{11000 MeV}{106.031 MeV} (.511 MeV) \approx -53.013 MeV
\end{cases}[/math]
[math]\Longrightarrow \left( \begin{matrix} E^*_{1}\\ p^*_{1(x)} \\ p^*_{1(y)} \\ p^*_{1(z)}\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^* \gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E_{1}\\ 0 \\ 0 \\ p_{1(z)}\end{matrix} \right)[/math]
[math]\Longrightarrow\begin{cases}
E^*_{1}=\gamma^* (E_{1})-\beta^* \gamma^* p_{1(z)} \\
p^*_{1(z)}=-\beta^* \gamma^*(E_{1})+\gamma^* p_{1(z)}
\end{cases}[/math]
[math]\Longrightarrow\begin{cases}
E^*_{1}=\frac{(E_{1}+m)}{E^*} (E_{1})-\frac{p_{1(z)}}{(E_{1}+m)} \frac{(E_{1}+m)}{E^*} p_{1(z)} \\
p^*_{1(z)}=-\frac{p_{1}}{(E_{1}+m)} \frac{(E_{1}+m)}{E^*}(E_{1})+\frac{(E_{1}+m)}{E^*} p_{1(z)}
\end{cases}[/math]
[math]\Longrightarrow\begin{cases}
E^*_{1}=\frac{(11000 MeV+.511 MeV)}{106.031 MeV} (11000 MeV)-\frac{11000 MeV}{106.031 MeV} 11000 MeV \approx 53.015 MeV\\
p^*_{1(z)}=-\frac{11000 MeV}{106.031 MeV}(11000 MeV)+\frac{(11000 MeV+.511 MeV)}{106.031 MeV} 11000 MeV \approx 53.013 MeV
\end{cases}[/math]
[math]p^*_{1} =\sqrt {(p^*_{1(x)})^2+(p^*_{1(y)})^2+(p^*_{1(z)})^2} \Longrightarrow p^*_{1}=p^*_{1(z)}[/math]
[math]p^*_{2} =\sqrt {(p^*_{2(x)})^2+(p^*_{2(y)})^2+(p^*_{2(z)})^2} \Longrightarrow p^*_{2}=p^*_{2(z)}[/math]
This gives the momenta of the particles in the center of mass to have equal magnitude, but opposite directions.
Figure 5.1.3: Initial momentum for lab frame electron incident at 11GeV as seen in the center of mass frame.
Figure 5.1.4: Initial momentum for a lab frame stationary particle as seen in the center of mass frame.
Figure 5.1.5: Initial incoming angle theta for a lab frame electron incident at 11GeV as seen in the center of mass frame.
Figure 5.1.6: Initial incoming angle theta for a lab frame stationary electron as seen in the center of mass frame.
[math]\textbf{\underline{Navigation}}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]