Determining wire-phi correspondance

Detector Geometry

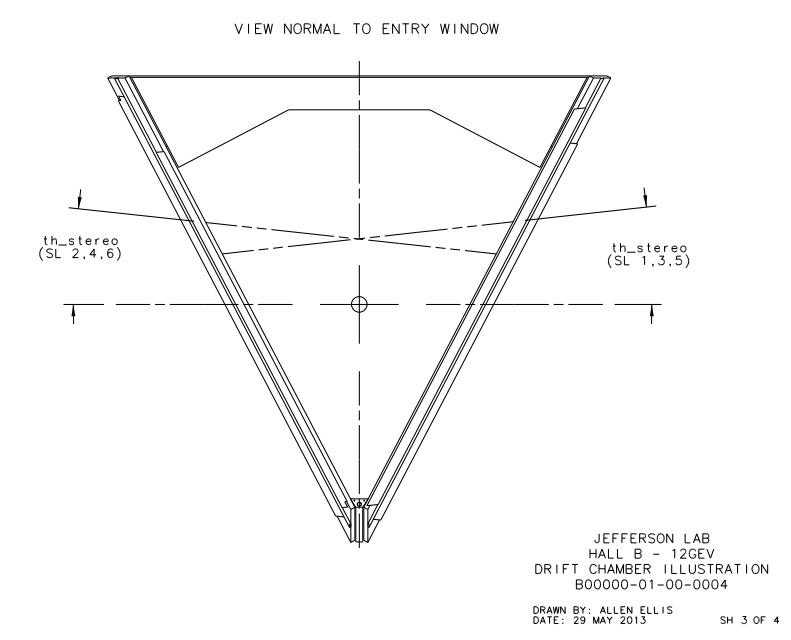
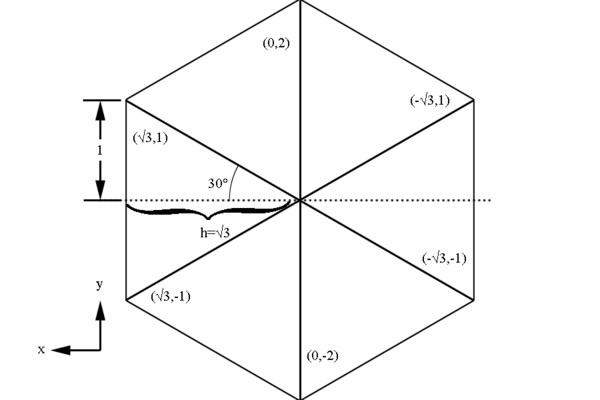
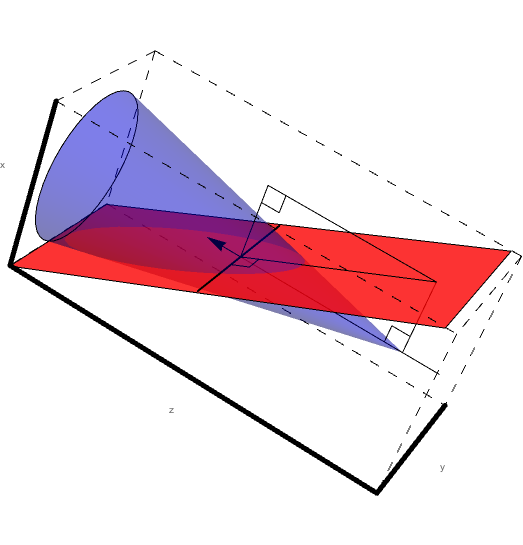
Examining the geometry of the Drift Chamber, we can see that the detector is similar to a hexagonal pyramid in shape.

Figure 1: A graphical rendering of a drift chamber sector.

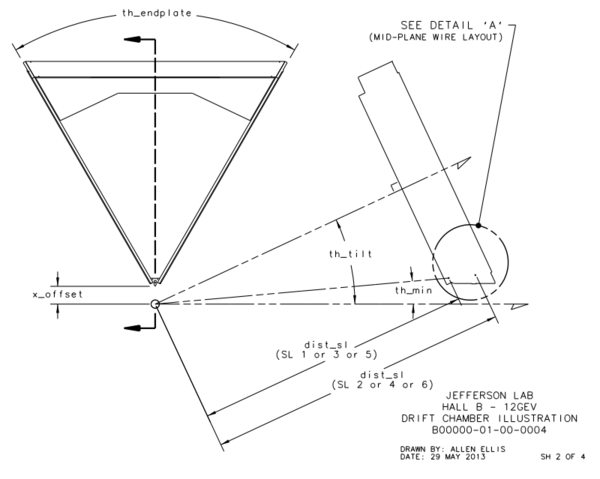
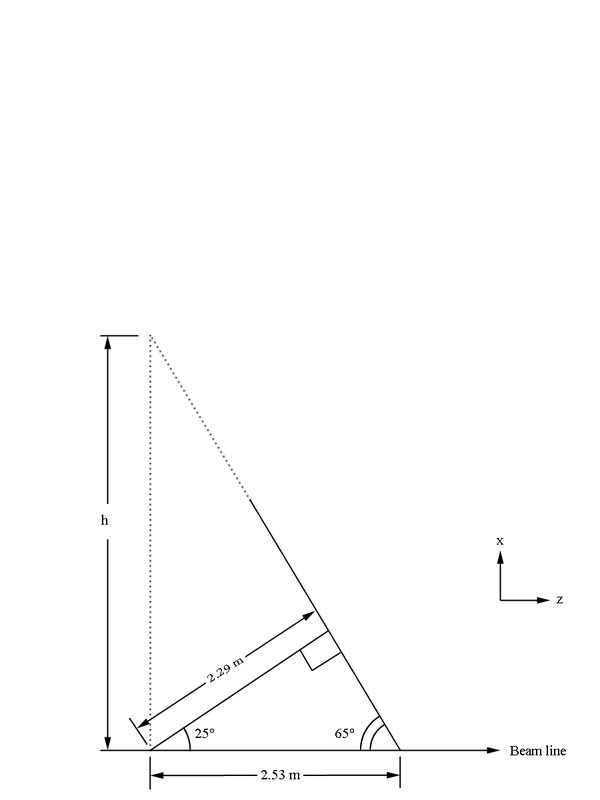
From the geometry it is given that xdist, the distance between the line of intersection of the two end-plate planes and the target position, is equal to 8.298 cm and th_min, the angle from the target vertex to the the same line, is 4.694 degrees. Using this knowledge we can simulate this situation by having the end-plate planes intersect at the beam line axis. This action in effect would grant the sector to measure angles below ~5 degrees, which we can account for by limiting angles theta within the accepted detector range. The quantity dist2tgt, the distance from the target to the first guard wire plane along the normal of said plane, is given as 228.078 cm. Using the previous understanding of the distances between planes within a Superlayer:

Figure 2: A graphical rendering of a drift chamber wire spacing.

We know that the seperation between levels is a constant D=.3861 cm, and that sensor layer 1 is 3 layers deep.

This gives us the distance to level 1 from the vertex (0,0,0) as 228.078 cm+3(0.3861) cm=229.2363 cm in the positive z direction along the beam line. Using the fact that the wire planes are at 25 degrees to the beam line, we can approximate sector one as triangle that intersects with a line perpendicular to the beam line at the vertex position of (0,0,0) along the bisector of the triangle. While this is beyond the physical constructs of the experimental design, we do this mathematical simplicity. This again is acceptable in that angles beyond the physical limitations of 40 degrees will not be simulated. From the geometry of a hexagonal pyramid, we can see that the quantity h should be

Figure 3: A graphical rendering of a drift chamber wire spacing from the side.

[math]h=2.292363\ m\ \cdot Tan(25^{\circ})[/math]

[math]h=1.07\ m[/math]

Examining the geometry of a hexagonal of h=[math]\sqrt{3}[/math] whose coordinates are easy to calculate:

Figure 4: A graphical rendering of a drift chamber geometry.

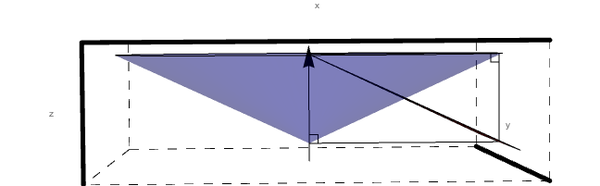
We can scale this hexagon by a factor of .617 to find the base of the hexagonal pyramid simulating the drift chamber geometry.

sector1=Graphics3D[{Red,Opacity[.8],Polygon[{{0,0,2.29},{.617\[Sqrt]3,.617,0},{.617\[Sqrt]3,-.617,0}}]},BoxStyle->Dashing[{0.02,0.02}],Axes->True,AxesLabel->{"x","y","z"},Ticks->None,AxesStyle->Thickness[0.01]];
sector2=Graphics3D[{GrayLevel[0.5],Opacity[.2],Polygon[{{0,0,2.29},{.617\[Sqrt]3,-.617,0},{0,-2*.617,0}}]},BoxStyle->Dashing[{0.02,0.02}],Axes->True,AxesLabel->{"x","y","z"},Ticks->None,AxesStyle->Thickness[0.01]];
sector3=Graphics3D[{GrayLevel[0.5],Opacity[.2],Polygon[{{0,0,2.29},{0,-2*.617,0},{-.617\[Sqrt]3,-.617,0}}]},BoxStyle->Dashing[{0.02,0.02}],Axes->True,AxesLabel->{"x","y","z"},Ticks->None,AxesStyle->Thickness[0.01]];
sector4=Graphics3D[{GrayLevel[0.5],Opacity[.2],Polygon[{{0,0,2.29},{-.617\[Sqrt]3,-.617,0},{-.617\[Sqrt]3,.617,0}}]},BoxStyle->Dashing[{0.02,0.02}],Axes->True,AxesLabel->{"x","y","z"},Ticks->None,AxesStyle->Thickness[0.01]];
sector5=Graphics3D[{GrayLevel[0.5],Opacity[.2],Polygon[{{0,0,2.29},{-.617\[Sqrt]3,.617,0},{0,2*.617,0}}]},BoxStyle->Dashing[{0.02,0.02}],Axes->True,AxesLabel->{"x","y","z"},Ticks->None,AxesStyle->Thickness[0.01]];
sector6=Graphics3D[{GrayLevel[0.5],Opacity[.2],Polygon[{{0,0,2.29},{0,2*.617,0},{.617\[Sqrt]3,.617,0}}]},BoxStyle->Dashing[{0.02,0.02}],Axes->True,AxesLabel->{"x","y","z"},Ticks->None,AxesStyle->Thickness[0.01]];
Bisector0Sector1=Graphics3D[Line[{{0,0,2.29},{.617\[Sqrt]3,0,0}}]];
Bisector0perpSector1=Graphics3D[Line[{{0,0,0},{.617\[Sqrt]3,0,0}}]];
RightAngleVertical=Graphics3D[Line[{{.25,0,.25},{.25,0,0}}]];
RightAngleHorizontal=Graphics3D[Line[{{.25,0,.25},{0,0,.25}}]];
Bisector0Cone=Graphics3D[Line[{{.617\[Sqrt]3,0,0},{.617\[Sqrt]3,0,2.29}}]];
Bisector0perpCone=Graphics3D[Line[{{0,0,2.29},{.617\[Sqrt]3,0,2.29}}]];
RightAngleVertical2=Graphics3D[Line[{{.617\[Sqrt]3-.25,0,2.29-.25},{.617\[Sqrt]3-.25,0,2.29}}]];
RightAngleHorizontal2=Graphics3D[Line[{{.617\[Sqrt]3-.25,0,2.29-.25},{.617\[Sqrt]3,0,2.29-.25}}]];
BeamLine=Graphics3D[Arrow[{{0,0,-.5},{0,0,2.79}}]];
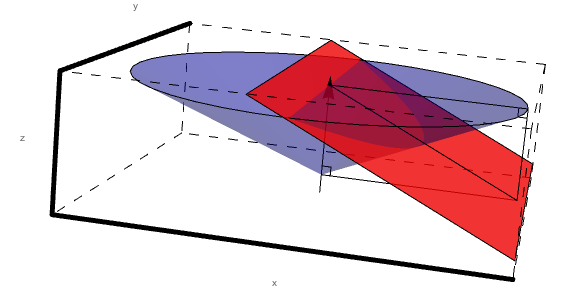
PhiCone=Graphics3D[{Blue,Opacity[.3],Cone[{{0,0,2.29},{0,0,0}},.617\[Sqrt]3]},BoxStyle->Dashing[{0.02,0.02}],Axes->True,AxesLabel->{"x","y","z"},Ticks->None,AxesStyle->Thickness[0.01]];

Viewing the simulation,

Show[sector1,sector2,sector3,sector4,sector5,sector6,PhiCone,BeamLine,Bisector0Sector1,Bisector0perpSector1,Bisector0Cone,Bisector0perpCone,RightAngleVertical,RightAngleHorizontal,RightAngleVertical2,RightAngleHorizontal2]

When the scattering angle theta, which is measured with respect to the beam line, is held constant and rotated through 360 degrees in phi, a cone is created. Using Mathematica, we can produce a 3D rendering of how the sectors for Level 1 would have to interact with a steady angle theta with respect to the beam line, as angle phi is rotated through 360 degrees.

Figure 5: A cone of constant Theta with varying Phi.

Conic Sections

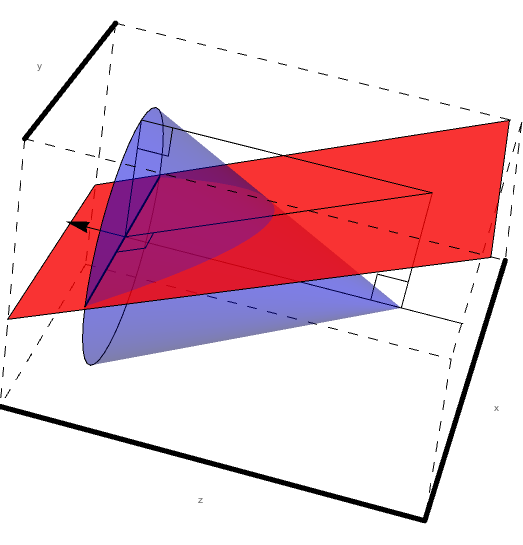
Looking just at sector 1, we can see that the intersection of level 1 and the cone of constant angle theta forms a conic section.

Show[sector1,PhiCone,BeamLine,Bisector0Sector1,Bisector0perpSector1,Bisector0Cone,Bisector0perpCone,RightAngleVertical,RightAngleHorizontal,RightAngleVertical2,RightAngleHorizontal2]

Figure 5: A cone of constant Theta with varying Phi.

Without loss of generalization, we can extend the triangle to an infinite plane to aid in viewing the conic section. Again, this falls outside of the experimental design range, but simulations would not occur in this forbidden zone.

sector1plane = 
  Graphics3D[{Red, Opacity[.8], 
    InfinitePlane[{{0, 0, 2.29}, {.617 \[Sqrt]3, .617, 
       0}, {.617 \[Sqrt]3, -.617, 0}}]}, 
   BoxStyle -> Dashing[{0.02, 0.02}], Axes -> True, 
   AxesLabel -> {"x", "y", "z"}, Ticks -> None, 
   AxesStyle -> Thickness[0.01]];

Figure 5: A cone of constant Theta with varying Phi.

Following the rules of conic sections we know that the eccentricity of the conic is given by:

[math]e=\frac{\sin \beta}{\sin\alpha}[/math]

where β is the angle between the plane and the horizontal and α is the angle between the cone's slant generator and the horizontal.

Examining the different conic sections possible we know that:

Circular Conic Section

If the conic is an circle, e=0. This implies

[math]e=\frac{\sin \beta}{\sin \alpha}=\frac{\sin\ (90^{\circ}-25^{\circ})}{\sin (90^{\circ}-\theta)}=0[/math]

Using the identity

[math]sin(90^{\circ}-t)=cos(t)[/math]

[math]\frac{cos (25^{\circ})}{0}=cos( \theta) =\infty[/math]

The sector angle will never be perpendicular to the plane of the light cone, so this is not a physical possibility.

Elliptic Conic Section

If the conic is an ellipse, 0<e<1. This implies

[math]e=\frac{\sin \beta}{\sin \alpha}=\frac{\sin\ (90^{\circ}-25^{\circ})}{\sin (90^{\circ}-\theta)}[/math]

Using the identity

[math]sin(90^{\circ}-t)=cos(t)[/math]

[math]\frac{cos (25^{\circ})}{cos (\theta)}=e[/math]

since e must be less than 1, this sets the limit of theta at less than 25 degrees. Similarly, since the limit of theta observed is 0 degrees, this sets the lower limit for the eccentricity

[math]\frac{cos (25^{\circ})}{cos (0)}=e=.9063078[/math]

This implies that the shape made on the the plane of the sector is an ellipse for angles

[math] 0\lt \theta\lt 25^{\circ}[/math]

Determining ellipse components

Figure 5: A cone of constant Theta with varying Phi.

Here we must take note of the fact that the center of the cone and the center of the ellipse do not coincide as can be shown visually by extending the cone length.

Figure 5: A cone of constant Theta with varying Phi.

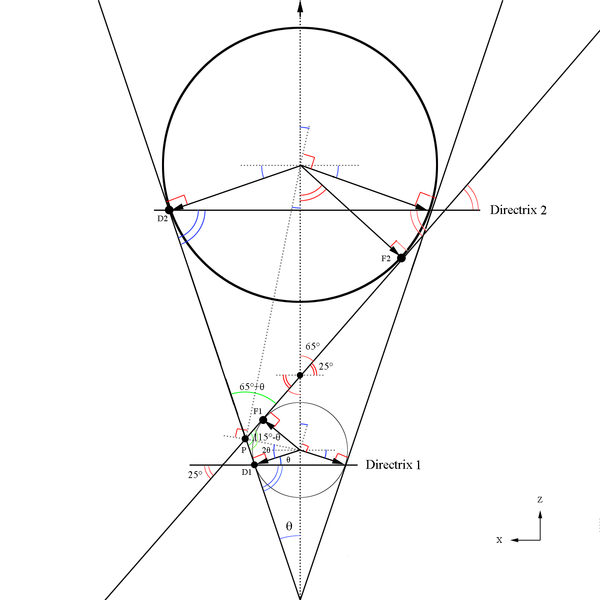
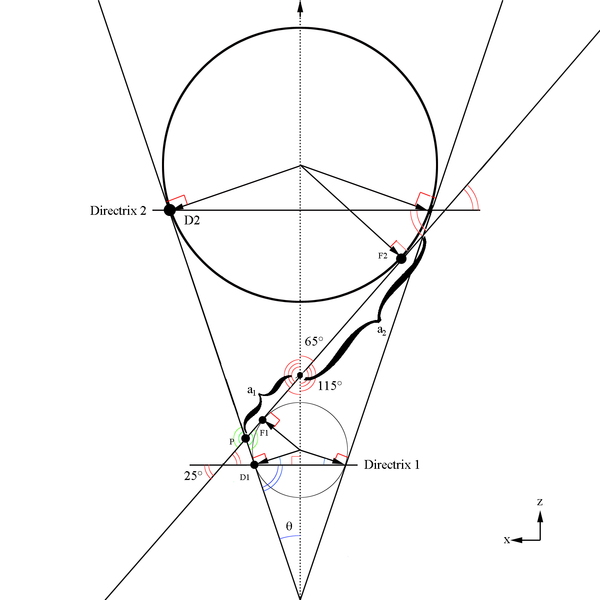
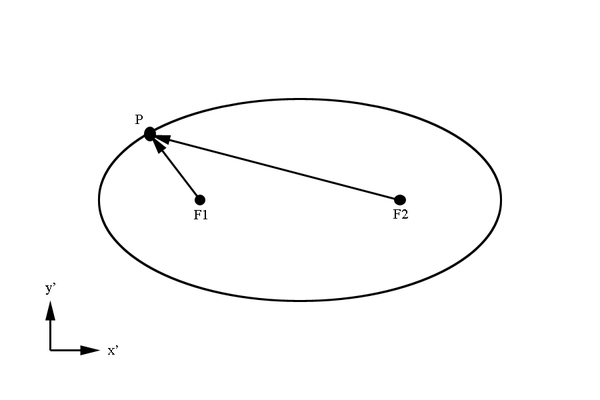
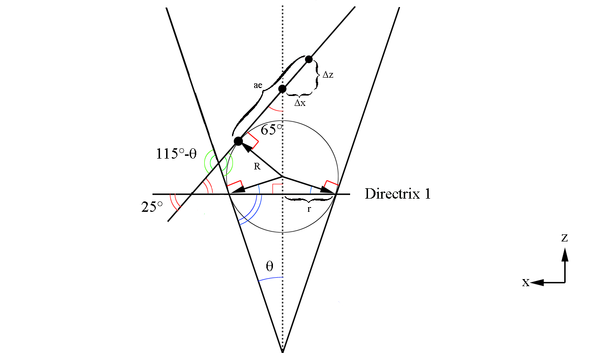
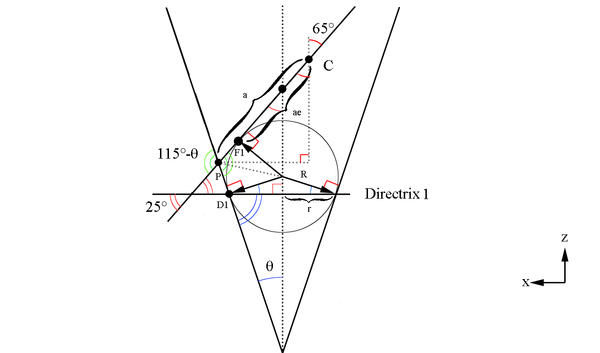
Here we will make use of Dandelin spheres to help determine the ellipse components with reference to the cone created at a constant theta. The basic construction of using Dandelin spheres is that within the cone, there are two spheres which are tangent to the plane as well as tangent to the cone as shown below in the xz plane. The Dandelin method picks an arbitrary point,P, on the intersection of the cone and the ellipse's plane. Drawing a line from the cone vertex through the point P, the directrix lines are intersected as shown below at D1 and D2. From the geometry as shown in the xz plane, it is shown that the line segments F1P=D1P and F2P=D2P since they share a common line segment, all three angles, and both have a the respective Dandelin radius as parts of the triangles they form.

Figure 5: A cone of constant Theta with varying Phi.

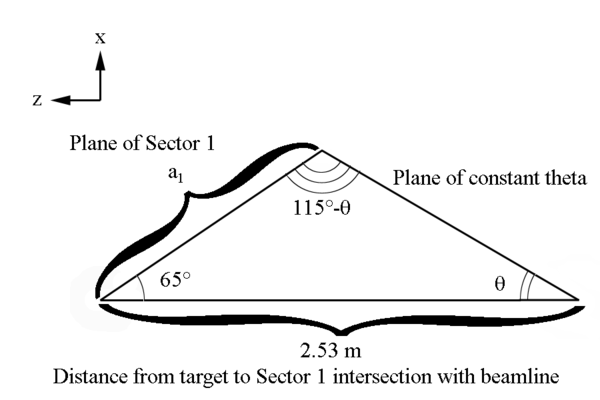
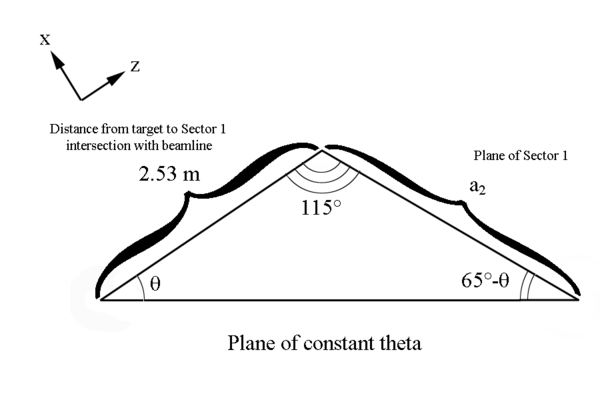
We can use the law of sines to find a portion of the ellipse

Figure 5: A cone of constant Theta with varying Phi.

[math]\frac{a}{sin(A)}=\frac{b}{sin(B)}[/math]

[math]\frac{2.29\ m}{sin(155^{\circ}-\theta)}=\frac{a_1}{sin(\theta)}[/math]

Figure 5: A cone of constant Theta with varying Phi.

[math]\frac{a}{sin(A)}=\frac{b}{sin(B)}[/math]

[math]\frac{2.29\ m}{sin(25^{\circ}-\theta)}=\frac{a_2}{sin(\theta)}[/math]

Since these lines meet at the intersection of each other, and they both originate at the vertex positions for the ellipse, we can state that the semi major axis is:

[math]2a\equiv a_1+a_2[/math]

Figure 5: A cone of constant Theta with varying Phi.

Using the fact that half the semi-major axis will give use the center of the ellipse

[math]a=\frac{a_1+a_2}{2}[/math]

[math]a=\frac{2.29sin(\theta)}{2}\left (\frac{sin(155^{\circ}-\theta)+sin(25^{\circ}-\theta)}{sin(155^{\circ}-\theta)sin(25^{\circ}-\theta)}\right )[/math]

Figure 5: A cone of constant Theta with varying Phi.

Earlier, using the law of sines it was found:

[math]\frac{2.29\ m}{sin(155^{\circ}-\theta)}=\frac{a_1}{sin(\theta)}[/math]

[math]\frac{2.29\ m \cdot sin(\theta)}{sin(155^{\circ}-\theta)}=a_1[/math]

Taking the difference

[math]\Delta a=a-a_1=\frac{a_1+a_2}{2}-a_1=\frac{a_2-a_1}{2}[/math]

[math]\Delta z=\Delta a \cdot cos(25^{\circ})[/math]

[math]\Delta x=\Delta a \cdot sin(25^{\circ})[/math]

Since the vertex position is at (0,0,0) this shows the center of the ellipse to be at

[math]c_{ellipse} \equiv (-\Delta a sin(25^{\circ}), 0,z+\Delta z)[/math]

[math]c_{ellipse} \equiv (-\Delta a sin(25^{\circ}), 0,2.29+\Delta z)[/math]

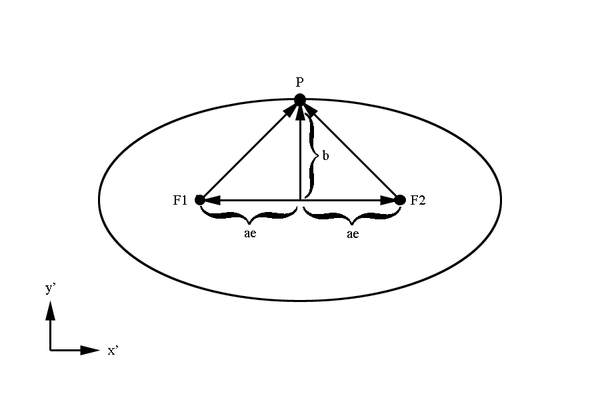
The sum of the distance from both focal points to a point on the surface of the ellipse is a constant

Figure 5: A cone of constant Theta with varying Phi.

[math]PF1+PF2\equiv 2a[/math]

A property of an ellipse is that the distance from the center of the ellipse to a focal point is given by

[math]f=ae=\left (\frac{a_1+a_2}{2}\right ) \left ( \frac{cos(25^{\circ})}{cos(\theta)}\right )[/math]

Figure 5: A cone of constant Theta with varying Phi.

[math]2ae+2b=2a\Rightarrow b=a(1-e)[/math]

[math]b=\left (\frac{a_1+a_2}{2}\right ) \left (1-\frac{cos(25^{\circ})}{cos(\theta)}\right )[/math]

[math]b=\frac{2.29sin(\theta)}{2}\left (\frac{sin(155^{\circ}-\theta)+sin(25^{\circ}-\theta)}{sin(155^{\circ}-\theta)sin(25^{\circ}-\theta)}\right ) \left (1-\frac{cos(25^{\circ})}{cos(\theta)}\right )[/math]

Additionally, using the fact that the distance from the center to a focal point is ae

Figure 5: A cone of constant Theta with varying Phi.

[math]R_{Lower\ Dandelin}=(ae-\Delta a) tan(25^{\circ})[/math]

[math]r_{D1}=R_{Lower\ Dandelin}cos(\theta)=(ae-\Delta a) tan(25^{\circ})cos(\theta)[/math]

By symmetry,

[math]R_{Upper\ Dandelin}=(ae+\Delta a) tan(25^{\circ})[/math]

[math]r_{D2}=R_{Lower\ Dandelin}cos(\theta)=(ae+\Delta a) tan(25^{\circ})cos(\theta)[/math]

Determining Elliptical Equation

As found earlier

Figure 5: A cone of constant Theta with varying Phi.

[math]CP_x=a\ sin(25^{\circ})[/math]

[math]CP_z=a\ cos(25^{\circ})[/math]

Given the center point coordinates found earlier:

[math]c \equiv (-\Delta x, 0,z+\Delta z)[/math]

[math]c \equiv (-\Delta a\ sin(25^{\circ}), 0,z+\Delta a\ cos(25^{\circ}))[/math]

This gives the location of P([math]\phi=0[/math]) at

[math]P(\phi=0) \equiv (-\Delta a\ sin(25^{\circ})+a\ sin((25^{\circ}), 0,z+\Delta a\ cos(25^{\circ})-a\ cos(25^{\circ}))[/math]

[math]P(\phi=0) \equiv (-\frac{a_2-a_1}{2} sin(25^{\circ})+\frac{a_1+a_2}{2} sin((25^{\circ}), 0,2.29+\frac{a_2-a_1}{2} cos(25^{\circ})-\frac{a_1+a_2}{2} cos(25^{\circ}))[/math]

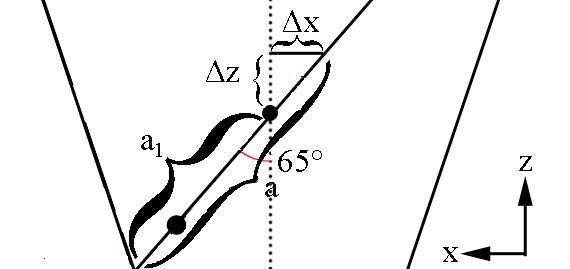
The height in z can be viewed as a linear function of x and expressed in slope intercept form for a plane:

[math]z_{Plane\ of\ sector}=m_{plane}x+b_{plane}[/math]

where

[math]m_{plane}=\frac{\Delta z}{\Delta x}=\frac{a\ cos(25^{\circ})}{-a\ sin(25^{\circ})}=-cot(25^{\circ})[/math]

[math]b_{plane}\equiv (0,0,2.29)[/math]

The D1 and D2 components can be obtained by finding the x and y components of the two directrix circles, which will be a function of their respective radii and the angle phi around the z axis.

[math]x_{Lower\ Directrix}^2+y_{Lower\ Directrix}^2=r_{Lower\ Directrix}^2\equiv r_{Lower\ Directrix}^2 cos^2(\phi)+r_{Lower\ Directrix}^2 sin^2(\phi)[/math]

Solving for the cartesian components,

[math]x_{Lower\ Directrix}=r_{Lower\ Directrix}\ cos(\phi)\qquad \qquad \qquad y_{Lower\ Directrix}=r_{Lower\ Directrix}\ sin(\phi)[/math]

Similarly,

[math]x_{Upper\ Directrix}=r_{Upper\ Directrix}\ cos(\phi)\qquad \qquad \qquad y_{Upper\ Directrix}=r_{Upper\ Directrix}\ sin(\phi)[/math]

Using the radius information found earlier for the upper and lower Dandelin spheres and directrix,

[math]R_{Lower\ Dandelin}=(ae-\Delta a) tan(25^{\circ})\qquad \qquad \qquad R_{Upper\ Dandelin}=(ae+\Delta a) tan(25^{\circ})[/math]

[math]r_{D1}=R_{Lower\ Dandelin}cos(\theta)=(ae-\Delta a) tan(25^{\circ})cos(\theta)\qquad \qquad\ \qquad r_{D2}=R_{Upper\ Dandelin}cos(\theta)=(ae+\Delta a) tan(25^{\circ})cos(\theta)[/math]

[math]r_{D1}=(\frac{a_1+a_2}{2}\frac{cos(25^{\circ})}{cos(\theta)}-\frac{a_2-a_1}{2}) tan(25^{\circ})cos(\theta)\qquad \qquad \qquad r_{D2}=(\frac{a_1+a_2}{2}\frac{cos(25^{\circ})}{cos(\theta)}+\frac{a_2-a_1}{2}) tan(25^{\circ})cos(\theta)[/math]

The height to the first directrix circle is

[math]z_{D1}=r_{D1}\ cot(\theta)[/math]

The height to the second directrix circle is

[math]z_{D2}=r_{D2}\ cot(\theta)[/math]

This gives the components for a point on the directrix circles as

[math]x_{D1}=(\frac{a_1+a_2}{2}\frac{cos(25^{\circ})}{cos(\theta)}-\frac{a_2-a_1}{2}) tan(25^{\circ})cos(\theta) cos(\phi)\qquad \qquad y_{D1}=(\frac{a_1+a_2}{2}\frac{cos(25^{\circ})}{cos(\theta)}-\frac{a_2-a_1}{2}) tan(25^{\circ})cos(\theta) sin(\phi)\qquad \qquad z_{D1}=r_{D1}\ cot(\theta)[/math]

[math]x_{D2}=(\frac{a_1+a_2}{2}\frac{cos(25^{\circ})}{cos(\theta)}+\frac{a_2-a_1}{2}) tan(25^{\circ})cos(\theta) cos(\phi)\qquad \qquad y_{D2}=(\frac{a_1+a_2}{2}\frac{cos(25^{\circ})}{cos(\theta)}+\frac{a_2-a_1}{2}) tan(25^{\circ})cos(\theta) sin(\phi)\qquad \qquad z_{D2}=r_{D2}\ cot(\theta)[/math]

Using these two points, which will be at the same angle phi around the z axis, a line can be created

[math]\vec d=r_{D2}cos(\phi)-r_{D1}cos(\phi)\ \hat x+r_{D2}sin(\phi)-r_{D1}sin(\phi)\ \hat y+r_{D2}cot(\theta)-r_{D1}cot(\theta)\ \hat z[/math]

Since this line is composed of the difference in the cartesian components of the two points it acts as a direction vector pointing from one point to the next. We can use the fact that a line in space is simply the intersection of two planes which in this situation results in the direction vector. Finding the parametric form equation of this line

[math](x,y,z)=(r_{D1}cos(\phi),\ r_{D1}sin(\phi),\ r_{D1}cot(\theta))+t(r_{D2}cos(\phi)-r_{D1}cos(\phi),\ r_{D2}sin(\phi)-r_{D1}sin(\phi),\ r_{D2}cot(\theta)-r_{D1}cot(\theta))[/math]

Solving for the individual cartesian components

[math]x=r_{D1}cos(\phi)+t(r_{D2}cos(\phi)-r_{D1}cos(\phi))\qquad \qquad y=r_{D1}sin(\phi)+t(r_{D2}sin(\phi)-r_{D1}sin(\phi))\qquad \qquad z=r_{D1}cot(\theta)+t(r_{D2}cot(\theta)-r_{D1}cot(\theta))[/math]

[math]\Rightarrow t=\frac{x-r_{D1}cos(\phi)}{r_{D2}cos(\phi)-r_{D1}cos(\phi)}=\frac{y-r_{D1}sin(\phi)}{r_{D2}sin(\phi)-r_{D1}sin(\phi)}=\frac{z-r_{D1}cot(\theta)}{r_{D2}cot(\theta)-r_{D1}cot(\theta)}[/math]

Since this condition implies that the 3 equations listed above for all conditions, we can solve for the [math]\phi=0[/math] situation which must then hold for all other instances of [math]\phi[/math]

[math]\frac{x-r_{D1}cos(\phi)}{r_{D2}cos(\phi)-r_{D1}cos(\phi)}=\frac{z-r_{D1}cot(\theta)}{r_{D2}cot(\theta)-r_{D1}cot(\theta)}[/math]

[math]\frac{x-r_{D1}cos(\phi)}{(r_{D2}-r_{D1})cos(\phi)}=\frac{z-r_{D1}cot(\theta)}{(r_{D2}-r_{D1})cot(\theta)}[/math]

[math]\frac{(x-r_{D1}cos(\phi))(r_{D2}-r_{D1})cot(\theta)}{(r_{D2}-r_{D1})cos(\phi)}+r_{D1}cot(\theta)=z[/math]

Using the condition that on the plane

[math]z_{plane}=cot(25^{\circ})x+2.29[/math]

We can substitute for z to find the point of intersection for the plane and cone at a given [math]\theta[/math] and [math]\phi[/math]

[math]\frac{ \left( x-r_{D1}cos(\phi) \right) cot(\theta)}{cos(\phi)}+r_{D1}cot(\theta)=-cot(25^{\circ})x+2.29[/math]

[math] \left ( \frac{x}{cos(\phi)}+r_{D1}-r_{D1} \right )cot(\theta )=-cot(25^{\circ})x+2.29[/math]

[math] \left ( \frac{x}{cos(\phi)} \right )cot(\theta )+cot(25^{\circ})x=2.29[/math]

[math] \frac{x\ cot(\theta )}{cos(\phi)}+cot(25^{\circ})x=2.29[/math]

[math] x \left (\frac{ cot(\theta)+cos(\phi)cot(25^{\circ})}{cos(\phi)}\right )=2.29[/math]

[math]x(cot(\theta)+cos(\phi)cot(25^{\circ})=2.29cos(\phi)[/math]

[math]x=\frac{2.29cos(\phi)}{(cot(\theta)+cos(\phi)cot(25^{\circ})}[/math]

Test for Theta [math]\theta=20^{\circ}[/math] and [math]\phi=0[/math]

Solving for the components of the ellipse

[math]a_1=\frac{2.29sin(\theta)}{sin(155-\theta)}=\frac{2.29sin(20^{\circ})}{sin(155^{\circ}-20^{\circ})}=\frac{2.29\cdot.342}{.707}=1.1076[/math]

[math]a_2=\frac{2.29sin(\theta)}{sin(25-\theta)}=\frac{2.29sin(20^{\circ})}{sin(25^{\circ}-20^{\circ})}=\frac{2.29\cdot.342}{.0872}=8.9865[/math]

[math]c_{ellipse} \equiv (-\Delta a\ sin(25^{\circ}), 0,z+\Delta a\ cos(25^{\circ}))[/math]

[math]c_{ellipse} \equiv (-\frac{a_2-a_1}{2} sin(25^{\circ}), 0,2.29+\frac{a_2-a_1}{2} cos(25^{\circ}))[/math]

[math]c_{ellipse} \equiv (-\frac{8.9865-1.1076}{2} sin(25^{\circ}), 0,2.29+\frac{8.9865-1.1076}{2} cos(25^{\circ}))[/math]

[math]c_{ellipse} \equiv (-\frac{7.8789}{2} sin(25^{\circ}), 0,2.29+\frac{7.8789}{2} cos(25^{\circ}))[/math]

[math]c_{ellipse} \equiv (-3.93945 sin(25^{\circ}), 0,2.29+3.93945 cos(25^{\circ}))[/math]

[math]c_{ellipse} \equiv (-1.6649, 0,5.86)[/math]

[math]P(\phi=0) \equiv (-\frac{8.9865-1.1076}{2} sin(25^{\circ})+\frac{1.1076+8.9865}{2} sin((25^{\circ}), 0,2.29+\frac{8.9865-1.1076}{2} cos(25^{\circ})-\frac{1.1076+8.9865}{2} cos(25^{\circ}))[/math]

[math]P(\phi=0) \equiv (-\frac{7.8789}{2} sin(25^{\circ})+\frac{10.0941}{2} sin((25^{\circ}), 0,2.29+\frac{7.8789}{2} cos(25^{\circ})-\frac{10.0941}{2} cos(25^{\circ}))[/math]

[math]P(\phi=0) \equiv (-3.93945 sin(25^{\circ})+5.04705 sin((25^{\circ}), 0,2.29+3.93945 cos(25^{\circ})-5.04705 cos(25^{\circ}))[/math]

[math]P(\phi=0) \equiv (.468, 0,1.29)[/math]

[math]x=\frac{2.29cos(\phi)-(r_{D2}-r_{D1})cos(\phi)cot(\theta)}{(cot(\theta)+cos(\phi)cot(25^{\circ})}[/math]

[math]x=\frac{2.29cos(0)-(3.8591-.407)cos(0)cot(20^{\circ})}{(cot(20^{\circ})+cos(0)cot(25^{\circ})}[/math]

[math]x=\frac{2.29-(3.4521\cdot 2.7475}{(2.7475+2.1445}[/math]

[math]x=\frac{2.29-(9.4846}{(4.89198}[/math]

[math]r_{D1}=R_{Lower\ Dandelin}cos(\theta)=(ae-\Delta a) tan(25^{\circ})cos(\theta)\qquad \qquad r_{D2}=R_{Lower\ Dandelin}cos(\theta)=(ae+\Delta a) tan(25^{\circ})cos(\theta)[/math]

[math]r_{D1}=(5.04705\cdot.96447-3.93945)\cdot .4663\cdot.9397=.407\ \text {cm} \qquad \qquad r_{D2}=(5.04705\cdot.96447+3.93945)\cdot .4663\cdot.9397=3.8591\ \text {cm}[/math]

The height to the first directrix circle is

[math]z_{D1}=r_{D1} cot(\theta)=.407cot(20)=1.12[/math]

and the x and y components are

[math]x_{D1}=r_{D1}\ cos(\phi)=.407 cos(0)=.407\text {cm}\ \ \ \ y_{D1}=r_{D1}cos(\phi)=.407 sin(0)=0[/math]

The height to the second directrix circle is

[math]z_{D2}=r_{D2} cot(\theta)=3.8591cot(20)=10.60\ \text{cm}[/math]

and the x and y components are

[math]x_{D2}=r_{D2} cos(\phi)=10.60cos(0)=10.60\text {cm}\ \ \ \ y_{D2}=r_{D2} sin(\phi)=10.60sin(0)=0[/math]

The distance between the two point

[math]\sqrt{(3.8591-.407)^2+(0-0)^2+(10.60-1.12)^2}=\sqrt{11.92+89.87}=10.09\text {cm}[/math]

This should be equal to 2a

[math]2a=2(\frac{(a_1+a_2}{2})=2(\frac{1.1076+8.9865}{2})=10.09\text {cm}[/math]

Using the fact that [math]c^2=a^2-b^2[/math]

[math]b^2=a^2-c^2=a^2-(ae)^2=a^2(1-e^2)[/math]

From the view point of the cone vertex looking down the beamline, the upper and lower directrix, as well as the ellipse at 25 degrees from the horizontal, appear as circles. The directrix circles share a center with the beamline/ cone vertex, while the ellipse's center is offset. This shows that if an angular measurement as in a rotation of phi were to occur, the circles and ellipse would not mark out the same angle.

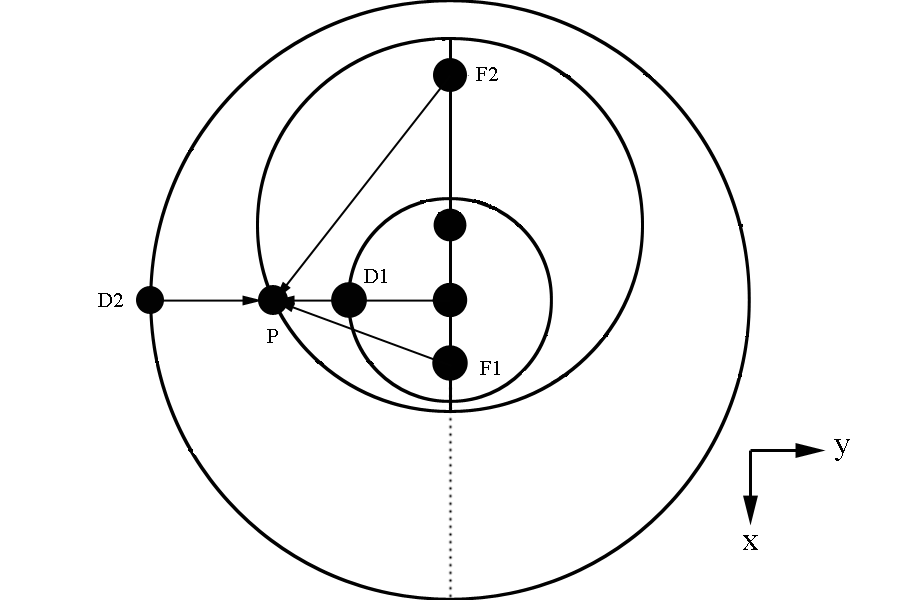
Using the properties of an ellipse, we can work in the coordinates of the ellipse where the center of the ellipse is at x'=0 and y'=0. The y and y' are equal, so for simplicity they are simply denoted as y.

[math]\Rightarrow F1P+F2P=2a[/math]

[math]\Rightarrow \sqrt{(x'+c_{x})^2+y^2}+\sqrt{(x'-c_{x})^2+y^2}=2a_x[/math]

[math](x'+c_x)^2+y^2=4a_x^2-4a_x\sqrt{(x'-c_x)^2+y^2}+(x'-c_x)^2+y^2[/math]

[math]\sqrt{(x'-c_x)^2+y^2}=4a_x^2-4a\sqrt{(x'-c_x)^2+y^2}+(x'-c_x)^2+y^2-(x'+c_x)^2+y^2[/math]

[math]\sqrt{(x'-c_x)^2+y^2}=\frac{4x'c_x-4a_x^2}{4a}[/math]

[math]\sqrt{(x'-c_x)^2+y^2}=a_x-\frac{c_xx'}{a_x}[/math] [math]x^{'2}-2x'c_x+c_x^2+y^2=a_x^2-2c_xx'+\frac{c_x^2x^{'2}}{a_x^2}[/math]

[math]\frac{x^{'2}(a_x^2-c_x^2)}{a_x^2}+y^2=a_x^2-c_x^2[/math]

[math]\frac{x^{'2}}{a_x^2}+\frac{y^2}{a_x^2-c_x^2}=1[/math]

where

[math]c \equiv a_xe\ sin(25^{\circ})[/math] [math]a_x^2-c_x^2\equiv b^2=a\ sin(25^{\circ})(1-e)[/math]

For ellipses centered at (h,k) in parallel to the beamline:

[math]\frac{(x-h)^2}{a_x^2}+\frac{(y-k)^2}{b^2}=1[/math]

[math]\frac{(x+\Delta a\ sin(25^{\circ}))^2}{a^2 sin^2(25^{\circ})}+\frac{(y)^2}{a^2\ sin^2(25^{\circ})(1-e)^2}=1[/math]

Substituting the parametric representation for x and y

[math]x=r\ cos(\phi)[/math]

[math]y=r\ sin(\phi)[/math]

[math]\theta\equiv 4.49876 +0.293001 n+0.000679074 n^2-3.57132\times 10^{-6} n^3[/math]

As discussed earlier, taking the 1st derivative of this function will give us the spacing of the bins as a function of wire number.

[math]\theta '\equiv 0.293001 + 0.00135815 n - 0.000010714 n^2[/math]

Parabolic Conic Section

If the conic is an parabola, e=1

This implies

[math]e=\frac{\sin \beta}{\sin \alpha}=\frac{\sin\ (90^{\circ}-25^{\circ})}{\sin (90^{\circ}-\alpha)}=1[/math]

Using the identity

[math]sin(90^{\circ}-t)=cos(t)[/math]

[math]\frac{cos (25^{\circ})}{1}=cos (\theta) [/math] [math]\theta=25^{\circ}[/math]

For a parabola:

[math]4px = y^2[/math]

where

p = distance from vertex to focus (or directrix)

Hyperbolic Conic Section

If the conic is an hyperbola, e>1

This implies

[math]e=\frac{\sin \beta}{\sin \alpha}=\frac{\sin\ (90^{\circ}-25^{\circ})}{\sin (90^{\circ}-\theta)}\gt 1[/math]

Using the identity

[math]sin(90^{\circ}-t)=cos(t)[/math]

[math]\frac{cos (25^{\circ})}{1}\gt cos (\theta) [/math]

[math]\theta\gt 25^{\circ}[/math]

Additionally, since the dector has an upward limit of 40 degres this implies that

[math]25^{\circ}\gt \theta\gt 40^{\circ}[/math]