Difference between revisions of "Niowave 9-2015"
(Created page with "The energy deposited by electrons scattered into a 3.48 diameter stainless steel beam pipe (1.65 mm thick) from a PbBi target as a function of a uniform Solenoidal magnetic fiel…") |
|||
| (10 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | Niowave Positron Project Progress for September 2015 | |
| + | |||
| + | |||
| + | Simulations were performed to predict the efficiency of producing positrons using a Lead-Bismuth target and a 10 MeV incident electron. MCNPX and GEANT4 were used to predict this efficiency in an effort to benchmark the results. Niowave performed a simulation using MCNPX and ISU used GEANT4. A comparison of the positron production efficiency predictions made by MCNPX and G4beamline (GEANT4) is shown in the table below. The two simulation packages appear to be consistent with each other for some thicknesses. | ||
| + | |||
| − | |||
{| border="1" | {| border="1" | ||
| − | + | | PbBi Thickness (mm) || #positrons/million electrons (G4Beamline)|| #positrons/million electrons (MCNPX) | |
| − | | | + | |- |
| + | | 1 ||1138,1154,1097,1159,1125 =1135<math>\pm</math>25 || 1091 | ||
| + | |- | ||
| + | | 1.5 || 1668,1701,1639, 1644, 1628=1656<math>\pm</math>29 ||1728 | ||
| + | |- | ||
| + | | 2 || 1937,1930,1851,1874,1945=1907<math>\pm</math>42 || 1984 | ||
| + | |- | ||
| + | | 3|| 1889,1821,1852,1809,1859=1846<math>\pm</math>32 || 1986 | ||
| + | |- | ||
| + | | 4||1726,1696,1673,1693,1681=1694<math>\pm</math> 20 || 1858 | ||
| + | |- | ||
| + | | 5|| 1566,1543,1546,1625,1566=1569<math>\pm</math>33 || 1646 | ||
| + | |- | ||
| + | | 6|| 1549, 1486,1564,1545,1452=1520<math>\pm</math> 50 ||1541 | ||
| + | |- | ||
| + | | 7|| 1462,1327, 1407,1489 ,1477=1432<math>\pm</math> 67 || 1541 | ||
| + | |- | ||
| + | |8|| 1289, 1335,1280, 1271, 1280 = 1291<math>\pm</math> 25 || | ||
| + | |- | ||
| + | | 10|| 1141,1241, 1199, 1202, 1148 =1186<math>\pm</math>42 || 1216 | ||
|- | |- | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | + | Below are the momentum distributions observed for both electrons and electrons using MCNPX. The 10 MeV electrons loose a mean energy of about 3 MeV traversing the 2mm thick PbBi target. The incident 10 MeV electrons produce Brehsstrahlung photons as traverse the PbBi target. These photon will produce electron-positron pairs within the PbBi target material. The positrons below escape the PbBi target and have a momentum between one and two MeV. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Electrons: | ||
| + | [[File:e01.png| 400 px]][[File:e02.png| 400 px]] | ||
| − | + | Positrons: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[File:p01.png| 400 px]][[File:p02.png| 400 px]] | |
| − | |||
Latest revision as of 14:39, 13 April 2016
Niowave Positron Project Progress for September 2015
Simulations were performed to predict the efficiency of producing positrons using a Lead-Bismuth target and a 10 MeV incident electron. MCNPX and GEANT4 were used to predict this efficiency in an effort to benchmark the results. Niowave performed a simulation using MCNPX and ISU used GEANT4. A comparison of the positron production efficiency predictions made by MCNPX and G4beamline (GEANT4) is shown in the table below. The two simulation packages appear to be consistent with each other for some thicknesses.
| PbBi Thickness (mm) | #positrons/million electrons (G4Beamline) | #positrons/million electrons (MCNPX) |
| 1 | 1138,1154,1097,1159,1125 =113525 | 1091 |
| 1.5 | 1668,1701,1639, 1644, 1628=165629 | 1728 |
| 2 | 1937,1930,1851,1874,1945=190742 | 1984 |
| 3 | 1889,1821,1852,1809,1859=184632 | 1986 |
| 4 | 1726,1696,1673,1693,1681=1694 20 | 1858 |
| 5 | 1566,1543,1546,1625,1566=156933 | 1646 |
| 6 | 1549, 1486,1564,1545,1452=1520 50 | 1541 |
| 7 | 1462,1327, 1407,1489 ,1477=1432 67 | 1541 |
| 8 | 1289, 1335,1280, 1271, 1280 = 1291 25 | |
| 10 | 1141,1241, 1199, 1202, 1148 =118642 | 1216 |
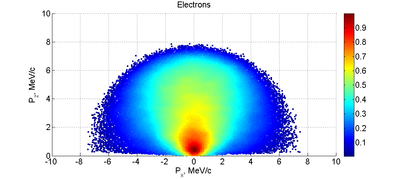
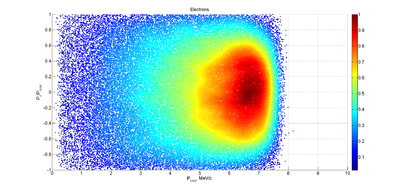
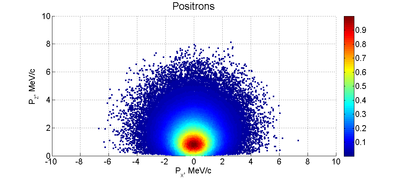
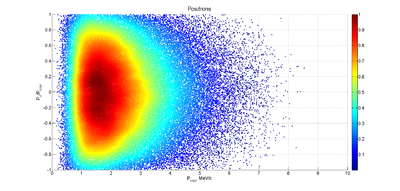
Below are the momentum distributions observed for both electrons and electrons using MCNPX. The 10 MeV electrons loose a mean energy of about 3 MeV traversing the 2mm thick PbBi target. The incident 10 MeV electrons produce Brehsstrahlung photons as traverse the PbBi target. These photon will produce electron-positron pairs within the PbBi target material. The positrons below escape the PbBi target and have a momentum between one and two MeV.
Electrons:
Positrons: