Difference between revisions of "Reconstructing Moller Events"
| Line 160: | Line 160: | ||
<center><math>\therefore E^*=E_1^*+E_2^* \Longrightarrow E_1^*=E_2^*</math></center> | <center><math>\therefore E^*=E_1^*+E_2^* \Longrightarrow E_1^*=E_2^*</math></center> | ||
| + | |||
| + | Since the energies are equal, we use this fact to find the momenta | ||
| + | |||
| + | |||
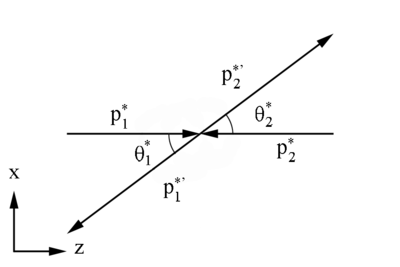
| + | <center><math>|p_1^*|=\sqrt{E_1^{*2}-m^{*2}}</math></center> | ||
=Alter Phi Angles= | =Alter Phi Angles= | ||
=Run for Necessary Amount to match Cross Section= | =Run for Necessary Amount to match Cross Section= | ||
Revision as of 17:26, 4 February 2016
Setup
Since we want to run for a evenly spaced energy range for Moller electrons, we will need to use some of the scattered electrons to help cover this range. A Moller scattering data file of 1E7 events has no Moller electrons with momentum over 5500 MeV. Since momentum is conserved, and the data is verified kinematicly verified, we can simply "switch" the data. This data can then be altered to have a certain number of different phi values for each energy to match the Moller cross section. This data can then be written to a LUND file, and compared to the previous calculations which did not factor in loss of initial energy.
Prepare Data
Using the existing Moller scattering data from a GEANT simulation of 4E7 incident electrons, a file of just scattered momentum components can be constructed using:
awk '{print $9, $10, $11, $16, $17, $18}' MollerScattering_NH3_Large.dat > Just_Scattered_Momentum.dat
Transfer to CM Frame
Center of Mass Frame
4-Momentum Invariants
Starting with the definition for the total relativistic energy:
Since we can assume that the frame of reference is an inertial frame, it moves at a constant velocity, the mass should remain constant.
We can use 4-momenta vectors, i.e. ,with c=1, to describe the variables in the CM Frame.
Using the fact that the scalar product of a 4-momenta with itself,
is invariant.
Using this notation, the sum of two 4-momenta forms a 4-vector as well
The length of this four-vector is an invariant as well
Equal masses
For incoming electrons moving only in the z-direction, we can write
We can perform a Lorentz transformation to the Center of Mass frame, with zero total momentum
Without knowing the values for gamma or beta, we can utalize the fact that lengths of the two 4-momenta are invariant
This gives,
Using the fact that
since the rest mass energy of the electrons remains the same in inertial frames.
Substituting, we find
This confirms that the mass remains constant between the frames of reference.
Total Energy in CM
Setting the lengths of the 4-momenta equal to each other,
we can use this for the collision of two particles of mass m. Since the total momentum is zero in the Center of Mass frame, we can express total energy in the center of mass frame as
Scattered / Moller Electron energies and momenta in CM
By the definition of the CM Frame we know
Using the relativistic definition of total energy:
Since the energies are equal, we use this fact to find the momenta