Difference between revisions of "Scattering Cross Section"
| Line 75: | Line 75: | ||
We can use the Jacobian to find the transformation term on the right | We can use the Jacobian to find the transformation term on the right | ||
| − | <center><math>J=\frac{\partial p_{CM}\partial \cos{\theta_{CM})}}{\partial p_{Lab}\partial \cos{\theta_{Lab})}}</math></center> | + | <center><math>J=\frac {\partial p_{CM}\partial \cos{\theta_{CM})}}{\partial p_{Lab}\partial \cos{\theta_{Lab})}}</math></center> |
| + | |||
=\begin{vmatrix} | =\begin{vmatrix} | ||
| − | \frac{\partial p_{CM}}{\partial p_{Lab}} & \frac{\partial p_{CM}}{\partial \cos{\theta_{Lab}) | + | \frac {\partial p_{CM}} {\partial p_{Lab}} & \frac {\partial p_{CM}} {\partial \cos{\theta_{Lab})} \\ |
z & v | z & v | ||
\end{vmatrix} | \end{vmatrix} | ||
<center><math>\left( \begin{matrix} E_1^*+E_2^* \\ p^*_{1(x)}+p^*_{2(x)} \\ p^*_{1(y)}+p^*_{2(y)} \\ p^*_{1(z)}+p^*_{2(z)}\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^*\gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E_{1}+E_{2}\\ p_{1(x)}+p_{2(x)} \\ p_{1(y)}+p_{2(y)} \\ p_{1(z)}+p_{2(z)}\end{matrix} \right)</math></center> | <center><math>\left( \begin{matrix} E_1^*+E_2^* \\ p^*_{1(x)}+p^*_{2(x)} \\ p^*_{1(y)}+p^*_{2(y)} \\ p^*_{1(z)}+p^*_{2(z)}\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^*\gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E_{1}+E_{2}\\ p_{1(x)}+p_{2(x)} \\ p_{1(y)}+p_{2(y)} \\ p_{1(z)}+p_{2(z)}\end{matrix} \right)</math></center> | ||
Revision as of 01:00, 3 February 2016
Scattering Cross Section
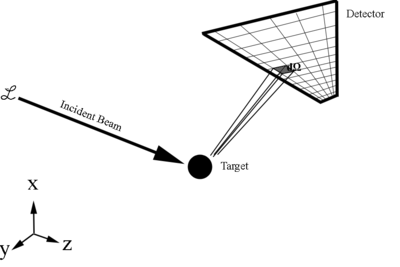
Since this is just a ratio of detected particles to total particles, this gives the cross section as a relative probablity of a scattering, or reaction, to occur.
Transforming Cross Section Between Frames
Transforming the cross section between two different frames of reference has the condition that the quantity must be equal in both frames. This is due to the fact that
This makes the total cross section a Lorentz invariant in that it is not effected by any relativistic transformations
This implies that the number of particles going into the solid-angle element d ΩLab and having a momentum between pLab and pLab+dpLabbe the same as the number going into the corresponding solid-angle element dΩCM and having a corresponding momentum between pCM and pCM+dpCM
As shown earlier,
We can use the fact that
We can use the Jacobian to find the transformation term on the right
=\begin{vmatrix} \frac {\partial p_{CM}} {\partial p_{Lab}} & \frac {\partial p_{CM}} {\partial \cos{\theta_{Lab})} \\ z & v \end{vmatrix}