Difference between revisions of "Scattering Cross Section"
Jump to navigation
Jump to search
| Line 12: | Line 12: | ||
<center><math>\Rightarrow \sigma=\int\limits_{\theta=0}^{\pi} \int\limits_{\phi=0}^{2\pi} \left(\frac{d\sigma}{d\Omega}\right)\ \sin{\theta}\,d\theta\,d\phi =\frac{N}{\mathcal L}\equiv total\ scattering\ cross\ section</math></center> | <center><math>\Rightarrow \sigma=\int\limits_{\theta=0}^{\pi} \int\limits_{\phi=0}^{2\pi} \left(\frac{d\sigma}{d\Omega}\right)\ \sin{\theta}\,d\theta\,d\phi =\frac{N}{\mathcal L}\equiv total\ scattering\ cross\ section</math></center> | ||
| + | |||
| + | Since this is just a ratio of detected particles to total particles, this gives the cross section as a relative probablity of a scattering, or reaction, to occur. | ||
=Transforming Cross Section Between Frames= | =Transforming Cross Section Between Frames= | ||
Revision as of 21:40, 2 February 2016
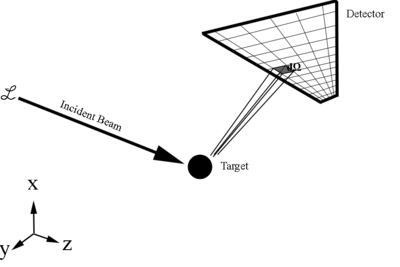
Scattering Cross Section

Since this is just a ratio of detected particles to total particles, this gives the cross section as a relative probablity of a scattering, or reaction, to occur.
Transforming Cross Section Between Frames
Transforming the cross section between two different frames of reference has the condition that the quantity must be equal in both frames. This is due to the fact that
This makes the total cross section a Lorentz invariant in that it is not effected by any relativistic transformations
This is that the number of particles going into the solid-angle element d\Omega and having a moentum between p and p+dp be the same as the number going into the correspoiding solid-angle element d\Omega^* and having a corresponding momentum between p^* and p*+dp*