Difference between revisions of "Scattering Cross Section"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
=Scattering Cross Section= | =Scattering Cross Section= | ||
| + | |||
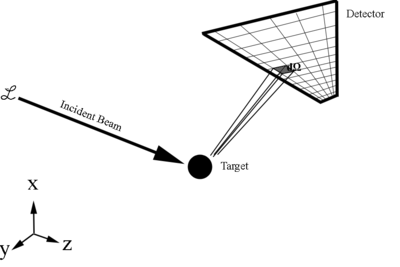
| + | <center>[[File:Scattering.png | 400 px]]</center> | ||
| + | |||
<center><math>\frac{d\sigma}{d\Omega} = \frac{\left(\frac{number\ of\ particles\ scattered/second}{d\Omega}\right)}{\left(\frac{number\ of\ incoming\ particles/second}{cm^2}\right)}=\frac{dN}{\mathcal L\, d\Omega} =differential\ scattering\ cross\ section</math></center> | <center><math>\frac{d\sigma}{d\Omega} = \frac{\left(\frac{number\ of\ particles\ scattered/second}{d\Omega}\right)}{\left(\frac{number\ of\ incoming\ particles/second}{cm^2}\right)}=\frac{dN}{\mathcal L\, d\Omega} =differential\ scattering\ cross\ section</math></center> | ||
| Line 5: | Line 8: | ||
<center><math>where\ d\Omega=\sin{\theta}\,d\theta\,d\phi</math></center> | <center><math>where\ d\Omega=\sin{\theta}\,d\theta\,d\phi</math></center> | ||
| − | |||
| − | |||
| − | |||
Revision as of 21:12, 2 February 2016
Scattering Cross Section

Transforming Cross Section Between Frames
Transforming the cross section between two different frames of reference has the condition that the quantity must be equal in both frames.
This is a Lorentz invariant.
Since the number of particles per second going into the detector is the same for both frames. (Only the z component of the momentum and the Energy are Lorentz transformed)
This is that the number of particles going into the solid-angle element d\Omega and having a moentum between p and p+dp be the same as the number going into the correspoiding solid-angle element d\Omega^* and having a corresponding momentum between p^* and p*+dp*