Difference between revisions of "Variables Used in Elastic Scattering"
Jump to navigation
Jump to search
where represents the 4-Momentum Vector in the CM frame
and represents the 4-Momentum Vector in the initial Lab frame
where represents the 4-Momentum Vector in the final Lab frame
| Line 41: | Line 41: | ||
<center><math>{\mathbf P_2}- {\mathbf P_2^'}= \left( \begin{matrix}E_2-E_2'\\ p_{2(x)}-p_{2(x)}^' \\ p_{2(y)}-p_{2(y)}^' \\ p_{2(z)}-p_{2(z)}^'\end{matrix} \right)={\mathbf P_d}</math></center> | <center><math>{\mathbf P_2}- {\mathbf P_2^'}= \left( \begin{matrix}E_2-E_2'\\ p_{2(x)}-p_{2(x)}^' \\ p_{2(y)}-p_{2(y)}^' \\ p_{2(z)}-p_{2(z)}^'\end{matrix} \right)={\mathbf P_d}</math></center> | ||
| − | Using the fact that the length of these 4-Momentum Vectors are invariant, | + | Using the algebraic fact |
| + | |||
| + | <center><math>\left({\mathbf a}- {\mathbf b}\right)^2=\left({\mathbf b- {\mathbf a}\right)^2</math></center> | ||
| + | |||
| + | |||
| + | and the fact that the length of these 4-Momentum Vectors are invariant, | ||
<center><math>\left({\mathbf P_1}- {\mathbf P_1^'}\right)^2= \left(\left( \begin{matrix}E_1-E_1'\\ p_{1(x)}-p_{1(x)}^' \\ p_{1(y)}-p_{1(y)}^' \\ p_{1(z)}-p_{1(z)}^'\end{matrix} \right)\right)^2=\left({\mathbf P_a}\right)^2</math></center> | <center><math>\left({\mathbf P_1}- {\mathbf P_1^'}\right)^2= \left(\left( \begin{matrix}E_1-E_1'\\ p_{1(x)}-p_{1(x)}^' \\ p_{1(y)}-p_{1(y)}^' \\ p_{1(z)}-p_{1(z)}^'\end{matrix} \right)\right)^2=\left({\mathbf P_a}\right)^2</math></center> | ||
| − | <center><math>{\mathbf P_1}- {\mathbf P_2^'}= \left( \begin{matrix}E_1-E_2'\\ p_{1(x)}-p_{2(x)}^' \\ p_{1(y)}-p_{2(y)}^' \\ p_{1(z)}-p_{2(z)}^'\end{matrix} \right)={\mathbf P_b}</math></center> | + | <center><math>\left({\mathbf P_1}- {\mathbf P_2^'}\right)^2= \left(\left( \begin{matrix}E_1-E_2'\\ p_{1(x)}-p_{2(x)}^' \\ p_{1(y)}-p_{2(y)}^' \\ p_{1(z)}-p_{2(z)}^'\end{matrix} \right)\right)^2=\left({\mathbf P_b}\right)^2</math></center> |
| − | <center><math>{\mathbf P_2}- {\mathbf P_1^'}= \left( \begin{matrix}E_2-E_1'\\ p_{2(x)}-p_{1(x)}^' \\ p_{2(y)}-p_{1(y)}^' \\ p_{2(z)}-p_{1(z)}^'\end{matrix} \right)={\mathbf P_c}</math></center> | + | <center><math>\left({\mathbf P_2}- {\mathbf P_1^'}\right)^2= \left(\left( \begin{matrix}E_2-E_1'\\ p_{2(x)}-p_{1(x)}^' \\ p_{2(y)}-p_{1(y)}^' \\ p_{2(z)}-p_{1(z)}^'\end{matrix} \right)\right)^2=\left({\mathbf P_c}\right)^2</math></center> |
| − | <center><math>{\mathbf P_2}- {\mathbf P_2^'}= \left( \begin{matrix}E_2-E_2'\\ p_{2(x)}-p_{2(x)}^' \\ p_{2(y)}-p_{2(y)}^' \\ p_{2(z)}-p_{2(z)}^'\end{matrix} \right)={\mathbf P_d}</math></center> | + | <center><math>\left({\mathbf P_2}- {\mathbf P_2^'}\right)^2= \left(\left( \begin{matrix}E_2-E_2'\\ p_{2(x)}-p_{2(x)}^' \\ p_{2(y)}-p_{2(y)}^' \\ p_{2(z)}-p_{2(z)}^'\end{matrix} \right)\right)^2=\left({\mathbf P_d}\right)^2</math></center> |
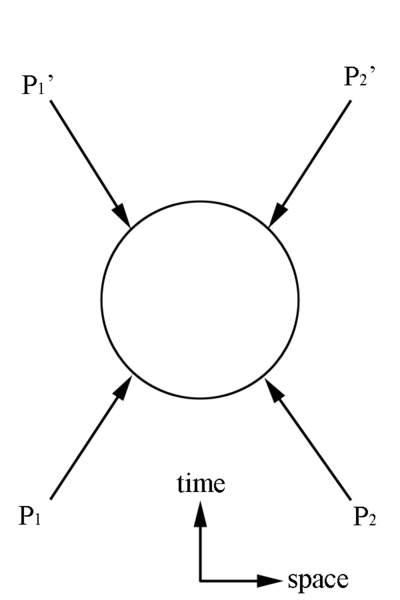
=Mandelstam Representation= | =Mandelstam Representation= | ||
[[File:Mandelstam.png | 400 px]] | [[File:Mandelstam.png | 400 px]] | ||
Revision as of 20:28, 31 January 2016
Lorentz Invariant Quantities
Total 4-Momentums
As was shown earlier the scalar product of a 4-Momentum vector with itself ,
,
and the length of a 4-Momentum vector composed of 4-Momentum vectors,
,
are invariant quantities.
It was further shown that
which can be expanded to
New 4-Momentum Quantities
Working in just the Lab frame, we can form new 4-Momentum Vectors comprised of 4-Momenta in this frame, with
Using the algebraic fact
and the fact that the length of these 4-Momentum Vectors are invariant,