Difference between revisions of "Variables Used in Elastic Scattering"
Jump to navigation
Jump to search
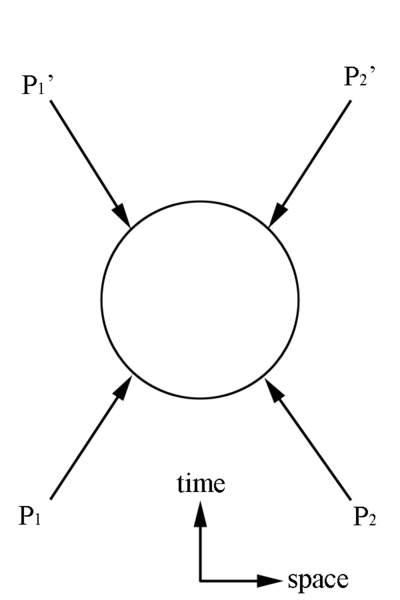
where represents the 4-Momentum Vector in the CM frame
and represents the 4-Momentum Vector in the initial Lab frame
where represents the 4-Momentum Vector in the final Lab frame
| Line 12: | Line 12: | ||
<center><math>{\mathbf P^*}^2={\mathbf P}^2</math></center> | <center><math>{\mathbf P^*}^2={\mathbf P}^2</math></center> | ||
| + | |||
<center>''where'' <math>{\mathbf P^*}=({\mathbf P_1^*}+{\mathbf P_2^*})^2</math> ''represents the 4-Momentum Vector in the CM frame''</center> | <center>''where'' <math>{\mathbf P^*}=({\mathbf P_1^*}+{\mathbf P_2^*})^2</math> ''represents the 4-Momentum Vector in the CM frame''</center> | ||
| + | |||
<center> ''and'' <math>{\mathbf P}=({\mathbf P_1}+{\mathbf P_2})^2</math> ''represents the 4-Momentum Vector in the initial Lab frame''</center> | <center> ''and'' <math>{\mathbf P}=({\mathbf P_1}+{\mathbf P_2})^2</math> ''represents the 4-Momentum Vector in the initial Lab frame''</center> | ||
| Line 20: | Line 22: | ||
<center><math>{\mathbf P^*}^2={\mathbf P}^2={\mathbf P^'}^2</math></center> | <center><math>{\mathbf P^*}^2={\mathbf P}^2={\mathbf P^'}^2</math></center> | ||
| + | |||
<center>''where'' <math>{\mathbf P^'}</math> ''represents the 4-Momentum Vector in the final Lab frame''</center> | <center>''where'' <math>{\mathbf P^'}</math> ''represents the 4-Momentum Vector in the final Lab frame''</center> | ||
Revision as of 19:37, 31 January 2016
Lorentz Invariant Quantities
As was shown earlier the scalar product of a 4-Momentum vector with itself ,
,
and the length of a 4-Momentum vector composed of 4-Momentum vectors,
,
are invariant quantities.
It was further shown that
which can be expanded to