Difference between revisions of "Variables Used in Elastic Scattering"
Jump to navigation
Jump to search
where represents the 4-Momentum Vector in the CM frame
and represents the 4-Momentum Vector in the initial Lab frame
where represents the 4-Momentum Vector in the final Lab frame
| Line 1: | Line 1: | ||
=Lorentz Invariant Quantities= | =Lorentz Invariant Quantities= | ||
As was [[DV_Calculations_of_4-momentum_components#4-Momentum_Invariants | shown earlier]] the scalar product of a 4-Momentum vector with itself ,<math>{\mathbf P_1}\cdot {\mathbf P^1}=E_1E_1-\vec p_1\cdot \vec p_1 =m_{1}^2=s</math> , and the length of a 4-Momentum vector composed of 4-Momentum vectors, <math>{\mathbf P^2}=({\mathbf P_1}+{\mathbf P_2})^2=(E_1+E_2)^2-(\vec p_1 +\vec p_2 )^2=(m_1+m_2)^2=s</math>, are invariant quantities. | As was [[DV_Calculations_of_4-momentum_components#4-Momentum_Invariants | shown earlier]] the scalar product of a 4-Momentum vector with itself ,<math>{\mathbf P_1}\cdot {\mathbf P^1}=E_1E_1-\vec p_1\cdot \vec p_1 =m_{1}^2=s</math> , and the length of a 4-Momentum vector composed of 4-Momentum vectors, <math>{\mathbf P^2}=({\mathbf P_1}+{\mathbf P_2})^2=(E_1+E_2)^2-(\vec p_1 +\vec p_2 )^2=(m_1+m_2)^2=s</math>, are invariant quantities. | ||
| + | |||
| + | It was [[DV_Calculations_of_4-momentum_components#Equal_masses | further shown ]] that | ||
| + | <center><math>{\mathbf P^*}^2={\mathbf P}^2</math></center> | ||
| + | <center>where <math>{\mathbf P^*}</math> represents the 4-Momentum Vector in the CM frame</center> | ||
| + | <center> and <math>{\mathbf P}</math> represents the 4-Momentum Vector in the initial Lab frame</center> | ||
| + | |||
| + | which can be expanded to | ||
| + | |||
| + | <center><math>{\mathbf P^*}^2={\mathbf P}^2={\mathbf P^'}^2</math></center> | ||
| + | |||
| + | <center>where <math>{\mathbf P^'}</math> represents the 4-Momentum Vector in the final Lab frame</center> | ||
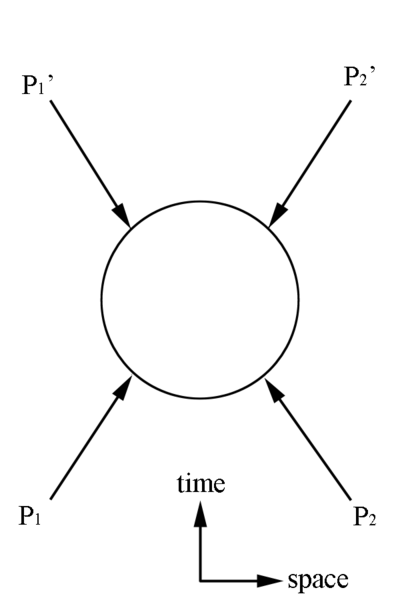
=Mandelstam Representation= | =Mandelstam Representation= | ||
[[File:Mandelstam.png | 400 px]] | [[File:Mandelstam.png | 400 px]] | ||
Revision as of 19:23, 31 January 2016
Lorentz Invariant Quantities
As was shown earlier the scalar product of a 4-Momentum vector with itself , , and the length of a 4-Momentum vector composed of 4-Momentum vectors, , are invariant quantities.
It was further shown that
which can be expanded to