|
|
| Line 349: |
Line 349: |
| | | | |
| | ===Different p<sub>2</sub><sup>1</sup> Values=== | | ===Different p<sub>2</sub><sup>1</sup> Values=== |
| | + | {| class="wikitable" align="center" border=1 |
| | + | |+ '''Differential Cross Section Scale for Different p<sub>2</sub><sup>1</sup> Values''' |
| | + | |- |
| | + | ! <math>p_{2}'</math> |
| | + | ! <math>\frac{d\omega}{d\Omega_{2}^'}</math> |
| | + | |- |
| | + | | 10000 MeV |
| | + | | |
| | + | |- |
| | + | | 5000 MeV |
| | + | | |
| | + | |- |
| | + | | 1000 MeV |
| | + | | |
| | + | |- |
| | + | | 500 MeV |
| | + | | |
| | + | |} |
| | | | |
| | ===Substituting for Moller range and energies=== | | ===Substituting for Moller range and energies=== |
Moller Lund
LUND file with Moller events (with origin of coordinates occurring at each event)
2 1 1 1 1 0 0.000563654 3.53715 0 6.2002
1 -1 1 11 0 0 0.69 -2.4999 10993.7998 10993.80 0.000511 0 0 0
2 -1 1 11 0 0 -0.69 2.4999 6.5852 7.08 0.000511 0 0 0
From a GEMC run WITH the Solenoid ced is used to obtain the information from the eg12_rec.ev file.

We take the phi angle from the Generated Event momentum as the initial phi angle. The obtain the final phi angle, we can look at the final position of the electron with in the drift chambers.

Examining the position from Timer Based Tracking, we can see that after rotations about first the y-axis, then the z-axis transforms from the detector frame of reference to the lab frame of reference.
Euler Angles
We can use the Euler angles to perform the rotations.
For the rotation about the y axis.
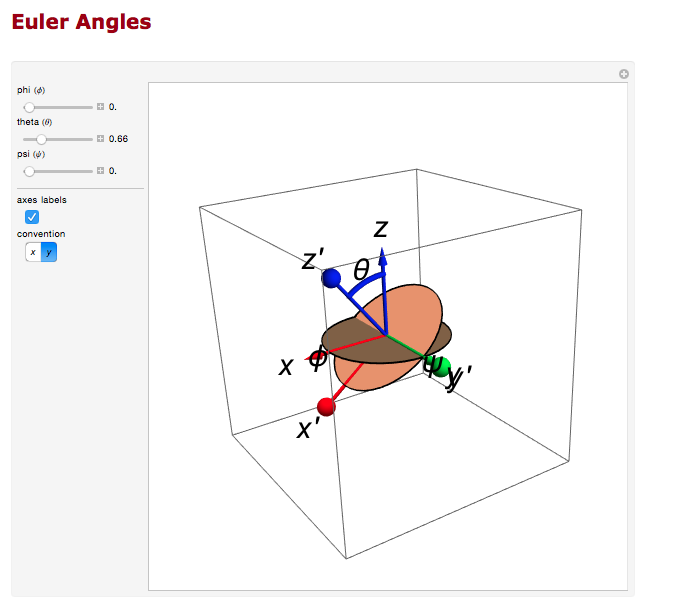
And the rotation about the z axis.
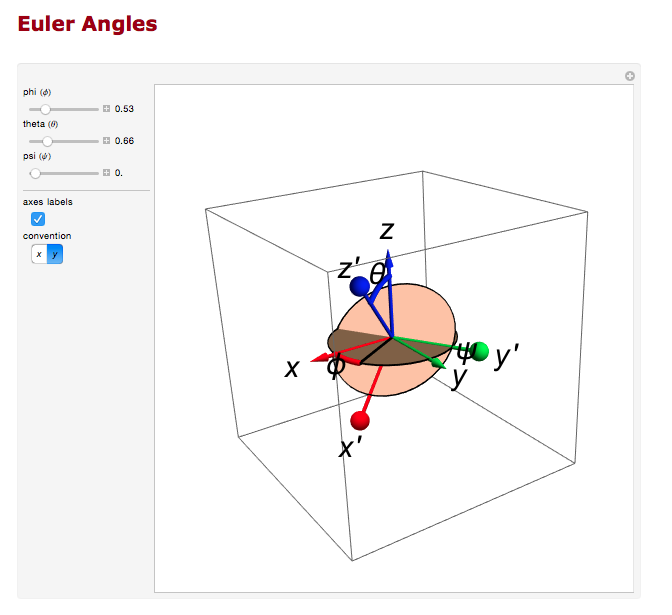
Transformation Matrix
The Euler angles can be applied using a transformation matrix
[math]\left(
\begin{array}{ccc}
\cos (\theta ) & 0 & -\sin (\theta ) \\
0 & 1 & 0 \\
\sin (\theta ) & 0 & \cos (\theta ) \\
\end{array}
\right).\left(
\begin{array}{c}
x \\
y \\
z \\
\end{array}
\right)[/math]
[math]=\left(
\begin{array}{c}
x \cos (\theta )-z \sin (\theta ) \\
y \\
z \cos (\theta )+x \sin (\theta ) \\
\end{array}
\right)[/math]
For event #29, in sector 3, the location of the first interaction is given by
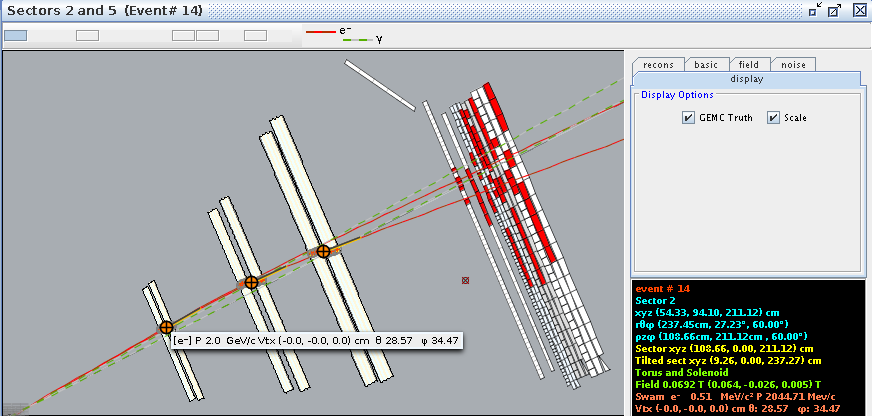
Converting -25 degrees to radians,
[math]\theta =-0.436332[/math]
which is the rotation the detectors are rotated from the y axis.
[math]\left(
\begin{array}{ccc}
\cos (\theta ) & 0 & -\sin (\theta ) \\
0 & 1 & 0 \\
\sin (\theta ) & 0 & \cos (\theta ) \\
\end{array}
\right).\left(
\begin{array}{c}
-15.76 \\
0 \\
237.43 \\
\end{array}
\right)[/math]
[math]=\left(
\begin{array}{c}
86.0588 \\
0. \\
221.845 \\
\end{array}
\right)[/math]
Finding [math]\phi =\frac{120\ 2 \pi }{360};[/math] since "sector -1" =3-1=2*60=120 degrees
[math]\left(
\begin{array}{ccc}
\cos (\phi ) & -\sin (\phi ) & 0 \\
\sin (\phi ) & \cos (\phi ) & 0 \\
0 & 0 & 1 \\
\end{array}
\right).\left(
\begin{array}{c}
86.0588 \\
0. \\
221.845 \\
\end{array}
\right)[/math]
[math]\left(
\begin{array}{c}
-43.0294 \\
74.5291 \\
221.845 \\
\end{array}
\right)[/math]
This shows how the coordinates are transformed and explains the validity of using the TBTracking information to obtain a phi angle in the lab frame.
Phi shifts
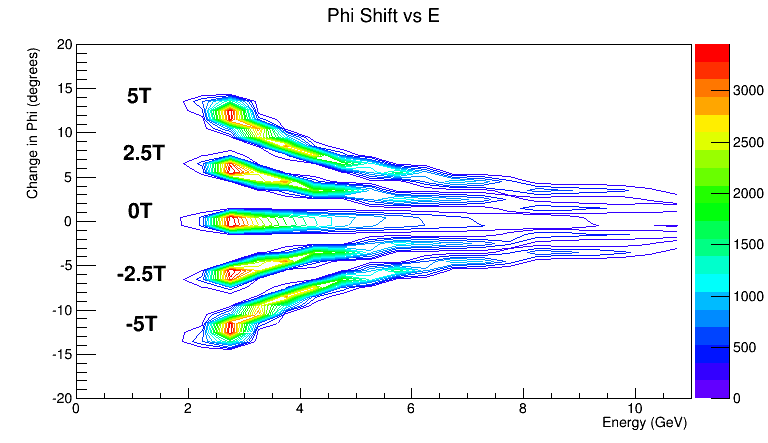
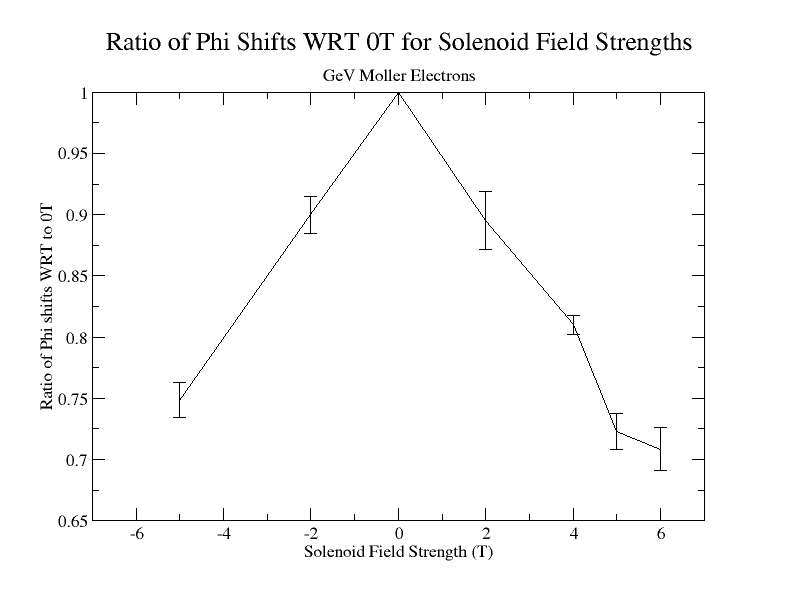
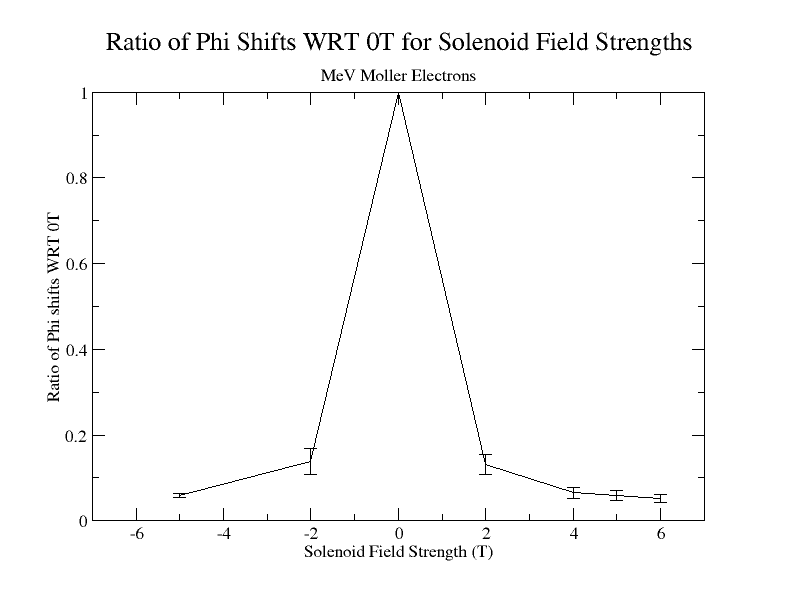
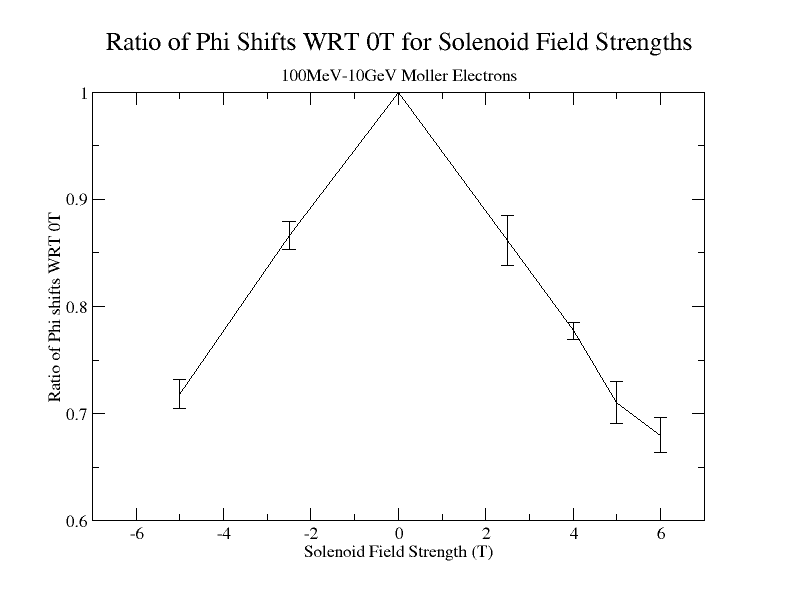
Cross-section Area
Calculations of 4-momentum components
DV_Calculations_of_4-momentum_components
Summary of 4-momentum calculations
| [math]For\ 0 \le \phi \le \frac{-\pi}{2}\ Radians[/math]
|
| x=POSITIVE
|
| y=NEGATIVE
|
| [math]For\ 0 \le \phi \le \frac{\pi}{2}\ Radians[/math]
|
| x=POSITIVE
|
| y=POSITIVE
|
| [math]For\ \frac{-\pi}{2} \le \phi \le -\pi\ Radians[/math]
|
| x=NEGATIVE
|
| y=NEGATIVE
|
| [math]For\ \frac{\pi}{2} \le \phi \le \pi\ Radians[/math]
|
| x=NEGATIVE
|
| y=POSITIVE
|
4 momentum calculations for different frames of reference
| Electron Initial Lab Frame
|
Moller electron Initial Lab Frame
|
Moller electron Final Lab Frame
|
Moller electron Center of Mass Frame
|
Electron Center of Mass Frame
|
Electron Final Lab Frame
|
| [math]p_{1}\equiv 11000 MeV[/math]
|
[math]p_{2}\equiv 0[/math]
|
[math]p_{2}'\equiv INPUT[/math]
|
[math]p_{2}^*=\sqrt{E_{2}^{*2}-m^2}[/math]
|
[math]p_{1}^*=\sqrt{E_{2}^{*2}-m^2}[/math]
|
[math]p_{1}'=\sqrt{E_{1}^{'\ 2}-m^2}[/math]
|
| [math]\theta_{1}\equiv 0[/math]
|
[math]\theta_{2}\equiv 0[/math]
|
[math]\theta_{2}'\equiv INPUT[/math]
|
[math]\theta_{2}^*=\arcsin \left(\frac{p_{2}'}{p_{2}^*}\ sin \left( \theta_{2}'\right) \right)[/math]
|
[math]\theta_{1}^*=\theta_{2}^*+\pi[/math]
|
[math]\theta_{1}'=\arcsin \left(\frac{p_{1}^*}{p_{1}'}\ sin \left( \theta_{1}^*\right) \right)[/math]
|
| [math]E_{1}=\sqrt{p_1^2+m^2}[/math]
|
[math]E_{2}\equiv m[/math]
|
[math]E_{2}'=\sqrt{p_{2}^{'\ 2}+m^2}[/math]
|
[math]E_{2}^*=\sqrt{\frac{m(m+E_1)}{2}}[/math]
|
[math]E_{1}^*=\sqrt{\frac{m(m+E_1)}{2}}[/math]
|
[math]E_{1}'\equiv E'-E_{2}'[/math]
|
| [math]p_{1(x)}\equiv 0[/math]
|
[math]p_{2(x)}\equiv 0[/math]
|
[math]p_{2(x)}'=\sqrt{p_{2}^{'\ 2}-p_{2(z)}^{'\ 2}} cos(\phi '_2)[/math]
|
[math]p_{2(x)}^*\equiv p_{2(x)}'[/math]
|
[math]p_{1(x)}^*\equiv-p_{2(x)}^*[/math]
|
[math]p_{1(x)}'\equiv p_{1(x)}^*[/math]
|
| [math]p_{1(y)}\equiv 0[/math]
|
[math]p_{2(y)}\equiv 0[/math]
|
[math]p_{2(y)}'=\sqrt{p_{2}^{'\ 2}-p_{2(x)}^{'\ 2}-p_{2(z)}^{'\ 2}}[/math]
|
[math]p_{2(y)}^*\equiv p_{2(y)}'[/math]
|
[math]p_{1(y)}^*\equiv -p_{2(y)}^*[/math]
|
[math]p_{1(y)}'\equiv p_{2(y)}^*[/math]
|
| [math]p_{1(z)}\equiv p_1[/math]
|
[math]p_{2(z)}\equiv 0[/math]
|
[math]p_{2(z)}'\equiv p_{2}'\ cos(\theta'_2)[/math]
|
[math]p_{2(z)}^*=\sqrt{p_{2}^{*\ 2}-p_{2(x)}^{*\ 2}-p_{2(y)}^{*\ 2}}[/math]
|
[math]p_{1(z)}^*\equiv -p_{2(z)}^*[/math]
|
[math]p_{1(z)}'=\sqrt{p_{1}^{'\ 2}-p_{(1(x)}^{'\ 2}-p_{1(y)}^{'\ 2}}[/math]
|
Differential Cross Section
Moller Differential Cross Section
Using the equation from [1]
[math]\frac{d\sigma}{d\Omega '_1}=\frac{ e^4 }{8E^{*2}}\left \{\frac{1+cos^4(\frac{\theta^*}{2})}{sin^4(\frac{\theta^*}{2})}+\frac{1+sin^4(\frac{\theta^*}{2})}{cos^4(\frac{\theta^*}{2})}+\frac{2}{sin^2(\frac{\theta^*}{2})cos^2(\frac{\theta^*}{2})} \right \}[/math]
[math]where\ \alpha=\frac{e^2}{\hbar c}\quad with\quad \hbar = c =1\ and\ \theta^*=\theta^*_1=\theta^*_2[/math]
This can be simplified to the form
[math]\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 }{4E^{*2}}\frac{ (3+cos^2\theta^*)^2}{sin^4\theta^*}[/math]
Plugging in the values expected for 2 scattering electrons:
[math]\alpha ^2=5.3279\times 10^{-5}[/math]
[math]E^*\approx 106.031 MeV[/math]
Using unit analysis on the term outside the parantheses, we find that the differential cross section for an electron at this momentum should be around
[math]\frac{5.3279\times 10^{-5}}{4\times 1.124\times 10^{16}eV^2}=1.18\times 10^{-21} eV^{-2}=\frac{1.18\times 10^{-21}}{1eV^2}\times \frac{1\times 10^{18} }{1\times 10^{18}}=\frac{.0012}{GeV^2}[/math]
Using the conversion of
[math]\frac{1}{1GeV^2}=.3894 mb[/math]
[math]\frac{.0012}{1GeV^2}=\frac{.0012}{1}\frac{1}{1GeV^2}=.0012\times .3894 mb=.467\times 10^{-3}mb[/math]
We find that the differential cross section scale is [math]\frac{d\sigma}{d\Omega}\approx .5\times 10^{-3}mb=.5\mu b[/math]
CM to Lab Frame
We can substitute in for [math]\theta[/math]
[math]\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 }{4E^{*2}}\frac{ (3+cos^2\theta^*)^2}{sin^4\theta^*}[/math]
[math]\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 }{4E^{*2}}\frac{ (3+cos^2\theta^*)^2}{sin(\theta^*)sin(\theta^*)sin(\theta^*)sin(\theta^*)}[/math]
Using,
[math]sin(\theta^*)=sin(\theta_{2}^*)=\frac{p_{2}'}{p_{2}^*}\ sin \left( \theta_{2}'\right)[/math]
[math]\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 }{4E^{*2}}\frac{ (3+cos^2\theta^*)^2}{\frac{p_{2}'}{p_{2}^*}\ sin \left( \theta_{2}'\right)\frac{p_{2}'}{p_{2}^*}\ sin \left( \theta_{2}'\right)\frac{p_{2}'}{p_{2}^*}\ sin \left( \theta_{2}'\right)\frac{p_{2}'}{p_{2}^*}\ sin \left( \theta_{2}'\right)}[/math]
[math]\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 p_{2}^{*4}}{4E^{*2}p_{2}'^4}\frac{ (3+cos^2\theta^*)^2}{sin^4 \left( \theta_{2}'\right)}[/math]
Now, using the trigometric identity,
[math]sin^2 t+cos^2 t=1\Longrightarrow cos^2(\theta^*)=1-sin^2(\theta^*)[/math]
[math]\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 p_{2}^{*4}}{4E^{*2}p_{2}'^4}\frac{ (3+1-sin^2(\theta^*))^2}{sin^4 \left( \theta_{2}'\right)}[/math]
[math]\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 p_{2}^{*4}}{4E^{*2}p_{2}'^4}\frac{ (4-sin(\theta^*)sin(\theta^*))^2}{sin^4 \left( \theta_{2}'\right)}[/math]
[math]\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 p_{2}^{*4}}{4E^{*2}p_{2}'^4}\frac{ (4-\frac{p_{2}'}{p_{2}^*}\ sin \left( \theta_{2}'\right)\frac{p_{2}'}{p_{2}^*}\ sin \left( \theta_{2}'\right))^2}{sin^4 \left( \theta_{2}'\right)}[/math]
[math]\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 p_{2}^{*4}}{4E^{*2}p_{2}'^4}\frac{ (4-\frac{p_{2}^{'2}}{p_{2}^{*2}}\ sin^2 \left( \theta_{2}'\right))^2}{sin^4 \left( \theta_{2}'\right)}[/math]
[math]\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 p_{2}^{*4}}{4E^{*2}p_{2}'^4}\frac{ (16-8\frac{p_{2}^{'2}}{p_{2}^{*2}}\ sin^2 \left( \theta_{2}'\right)+\frac{p_{2}^{'4}}{p_{2}^{*4}}\ sin^4 \left( \theta_{2}'\right))}{sin^4 \left( \theta_{2}'\right)}[/math]
Substituting,
[math]p_{2}^*=\sqrt{E_{2}^{*2}-m^2}[/math]
[math]\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 (\sqrt{E_{2}^{*2}-m^2})^4}{4E^{*2}p_{2}'^4}\frac{ (16-8\frac{p_{2}^{'2}}{p_{2}^{*2}}\ sin^2 \left( \theta_{2}'\right)+\frac{p_{2}^{'4}}{p_{2}^{*4}}\ sin^4 \left( \theta_{2}'\right))}{sin^4 \left( \theta_{2}'\right)}[/math]
[math]\frac{d\sigma}{d\Omega '_1}=\frac{ \alpha^2 (E_{2}^{*2}-m^2)^2}{4E^{*2}p_{2}'^4}\frac{ (16-8\frac{p_{2}^{'2}}{p_{2}^{*2}}\ sin^2 \left( \theta_{2}'\right)+\frac{p_{2}^{'4}}{p_{2}^{*4}}\ sin^4 \left( \theta_{2}'\right))}{sin^4 \left( \theta_{2}'\right)}[/math]
Substituting in for m, E2*,and E*
[math]\alpha^2=5.3279\times 10^{-5}[/math]
[math]\frac{d\sigma}{d\Omega '_1}=(\frac{ 5.3279\times 10^{-5}( ((53.015MeV)^{2}-(.511MeV)^2)^2}{4\times (106.031MeV)^{2}p_{2}'^4}\frac{ (16-8\frac{p_{2}^{'2}}{p_{2}^{*2}}\ sin^2 \left( \theta_{2}'\right)+\frac{p_{2}^{'4}}{p_{2}^{*4}}\ sin^4 \left( \theta_{2}'\right))}{sin^4 \left( \theta_{2}'\right)}[/math]
[math]\frac{d\sigma}{d\Omega '_1}=\frac{9.357\times 10^9}{p_{2}^{'4}}\frac{ (16-8\frac{p_{2}^{'2}}{p_{2}^{*2}}\ sin^2 \left( \theta_{2}'\right)+\frac{p_{2}^{'4}}{p_{2}^{*4}}\ sin^4 \left( \theta_{2}'\right))}{sin^4 \left( \theta_{2}'\right)}[/math]
Different p21 Values
Differential Cross Section Scale for Different p21 Values
| [math]p_{2}'[/math]
|
[math]\frac{d\omega}{d\Omega_{2}^'}[/math]
|
| 10000 MeV
|
|
| 5000 MeV
|
|
| 1000 MeV
|
|
| 500 MeV
|
|
Substituting for Moller range and energies
Converting the number of electrons to barns,
- [math]L=\frac{i_{scattered}}{\sigma} \approx i_{scattered}\times \rho_{target}\times l_{target}[/math]
where ρtarget is the density of the target material, ltarget is the length of the target, and iscattered is the number of incident particles scattered.
- [math]L=\frac{70.85 kg}{1 m^3}\times \frac{1 mole}{2.02 g} \times \frac{1000g}{1 kg} \times \frac{6\times10^{23} atoms}{1 mole} \times \frac{1cm}{100 cm} \times \frac{1 m}{ } \times \frac{10^{-23} m^2}{barn} =2.10\times 10^{-2} barns[/math]
- [math]\frac{1}{L \times 4\times 10^7}=1.19\times 10^{-6} barns[/math]
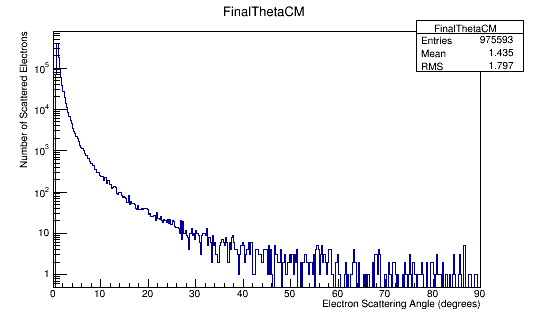
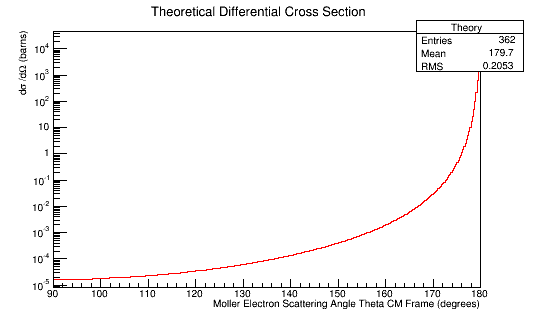
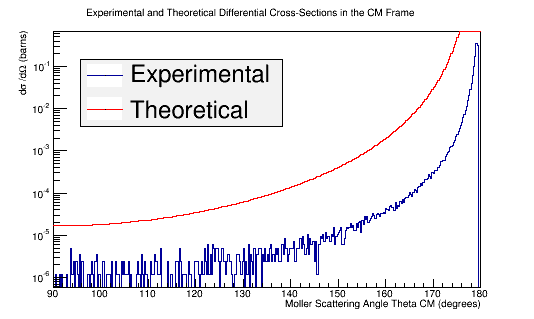
Combining these plots, and rescaling the Final Theta in the Center of Mass for micro-barns, we find
DV_RunGroupC_Moller#Moller_Track_Reconstruction











